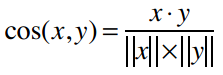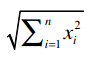依据欧几里得距离实现简易推荐功能

笔记

闵可夫斯基距离：

其中：

• r = 1 该公式即曼哈顿距离
• r = 2 该公式即欧几里得距离
• r = ∞ 极大距离

*r值越大，单个维度的差值大小会对整体距离有更大的影响。

 

 

皮尔逊相关系数用于衡量两个变量之间的相关性

它的值在-1至1之间，1表示完全吻合，-1表示完全相悖

有另外一个公式，能够计算皮尔逊相关系数的近似值：

这个公式虽然看起来更加复杂，而且其计算结果会不太稳定，有一定误差存在，但它最大的优点是，用代码实现的时候可以只遍历一次数据

 

 

 

应该使用哪种相似度？

• 如果数据存在“分数膨胀”问题，就使用皮尔逊相关系数。
• 如果数据比较“密集”，变量之间基本都存在公有值，且这些距离数据是非常重要的，那就使用欧几里得或曼哈顿距离。
• 如果数据是稀疏的，则使用余弦相似度。

其中，“·”号表示数量积。“||x||”表示向量x的模，计算公式是：

曼哈顿距离和欧几里得距离在数据完整的情况下会运作得非常好，如果数据比较稀疏，则要考虑使用余弦距离。

利用欧几里得距离实现简易推荐功能:

# -*- coding: utf-8 -*-
"""
Created on Mon Feb 28 09:52:22 2022

@author: Knight
"""

from math import sqrt


users = {"Angelica": {"Blues Traveler": 3.5, "Broken Bells": 2.0, "Norah Jones": 4.5, "Phoenix": 5.0, "Slightly Stoopid": 1.5, "The Strokes": 2.5, "Vampire Weekend": 2.0},
         "Bill":{"Blues Traveler": 2.0, "Broken Bells": 3.5, "Deadmau5": 4.0, "Phoenix": 2.0, "Slightly Stoopid": 3.5, "Vampire Weekend": 3.0},
         "Chan": {"Blues Traveler": 5.0, "Broken Bells": 1.0, "Deadmau5": 1.0, "Norah Jones": 3.0, "Phoenix": 5, "Slightly Stoopid": 1.0},
         "Dan": {"Blues Traveler": 3.0, "Broken Bells": 4.0, "Deadmau5": 4.5, "Phoenix": 3.0, "Slightly Stoopid": 4.5, "The Strokes": 4.0, "Vampire Weekend": 2.0},
         "Hailey": {"Broken Bells": 4.0, "Deadmau5": 1.0, "Norah Jones": 4.0, "The Strokes": 4.0, "Vampire Weekend": 1.0},
         "Jordyn":  {"Broken Bells": 4.5, "Deadmau5": 4.0, "Norah Jones": 5.0, "Phoenix": 5.0, "Slightly Stoopid": 4.5, "The Strokes": 4.0, "Vampire Weekend": 4.0},
         "Sam": {"Blues Traveler": 5.0, "Broken Bells": 2.0, "Norah Jones": 3.0, "Phoenix": 5.0, "Slightly Stoopid": 4.0, "The Strokes": 5.0},
         "Veronica": {"Blues Traveler": 3.0, "Norah Jones": 5.0, "Phoenix": 4.0, "Slightly Stoopid": 2.5, "The Strokes": 3.0}
        }


# 计算欧几里得距离
def ouji(rating1, rating2):
    commonRating = False
    
    sum = 0
    for r1 in rating1:
        if r1 in rating2:
            sum += (rating1[r1] - rating2[r1])**2
            commonRating = True
            
    distance = sqrt(sum)
    if commonRating:
        return distance
    else:
        return -1
    

# 得到欧几里得距离最小的用户
def getNearestUser(username, users):
    distances = []
    
    for user in users:
        if user != username:
            distance = ouji(users[user], users[username])
            distances.append((distance, user))
            
    distances.sort()
    return distances[0][1]


def recommend(username, users):
    nearest = getNearestUser(username, users)
    recomendations = []
    
    waitingList = users[nearest]
    doneList = users[username]
    for value in waitingList:
        if not value in doneList:
            recomendations.append((value, waitingList[value]))
            
    return recomendations
    

print( recommend("Chan", users))
# >>> [('The Strokes', 2.5), ('Vampire Weekend', 2.0)]

print( recommend("Jordyn", users))
# >>> [('Blues Traveler', 3.0)]