A - Fast Food Restaurant
一个比较复杂的模拟。不知道有没有贪心的做法。
struct Node {
int a, b, c;
} cnt[7];
void test_case() {
int A, B, C;
scanf("%d%d%d", &A, &B, &C);
int ans = 0;
for(int i = 0; i < (1 << 7); ++i) {
if(__builtin_popcount(i) > ans) {
int a = 0, b = 0, c = 0;
for(int x = 0; x < 7; ++x) {
if(i & (1 << x)) {
a += cnt[x].a;
b += cnt[x].b;
c += cnt[x].c;
}
}
if(a <= A && b <= B && c <= C)
ans = __builtin_popcount(i);
}
}
printf("%d
", ans);
}
cnt[0] = {1, 0, 0};
cnt[1] = {0, 1, 0};
cnt[2] = {0, 0, 1};
cnt[3] = {1, 1, 0};
cnt[4] = {0, 1, 1};
cnt[5] = {1, 0, 1};
cnt[6] = {1, 1, 1};
}
B - Different Rules
题意:有n个人,两次比赛,每次比赛每个人都获得一个[1,n]的独一无二的分数,两次比赛的分数之和就是总分数,在这题中,总分数越小的排名越靠前,总分数相同的并列为最后一个人的名次。例如:
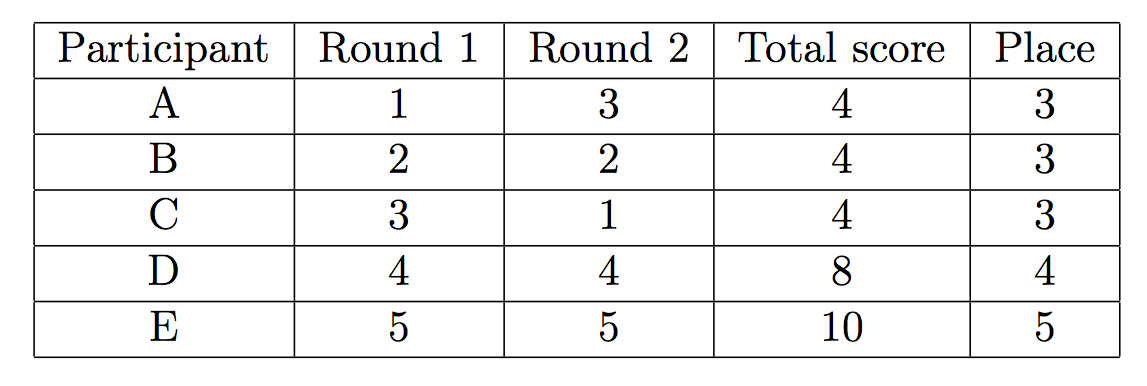
已知某个人的第一场的得分为x,第二场的得分为y,求他可能获得的最小名次以及最大名次。
题解:不失一般性,规定x<=y,且第i个人第一场获得的分数都是i。
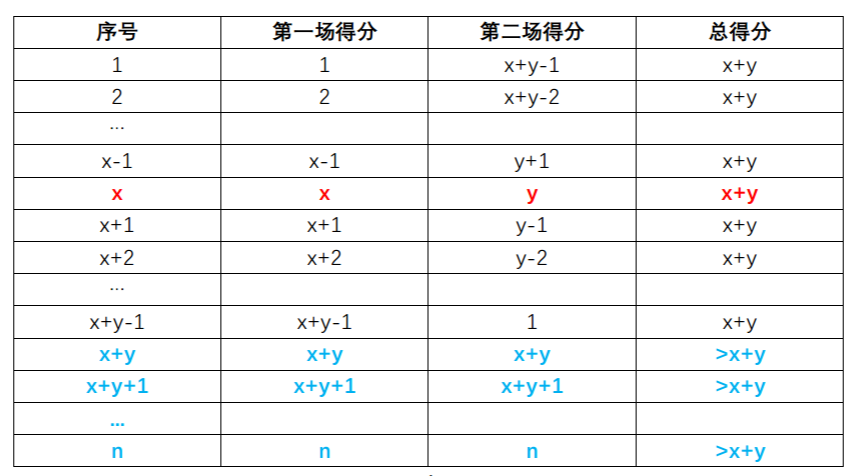
首先解决最小名次的情况,由于某个人的得分为x+y,所以尽可能构造x+y+1,因为得分要比他大,还要尽可能节约资源。所以是某段区间倒过来加,使得每个结果都是x+y+1,然后交换序号为x和x+1的两行,使得序号为x的行和为x+y,序号为x+1的行和为x+y+2,但是有一些边界情况。
当x+y<=n时,答案为1。
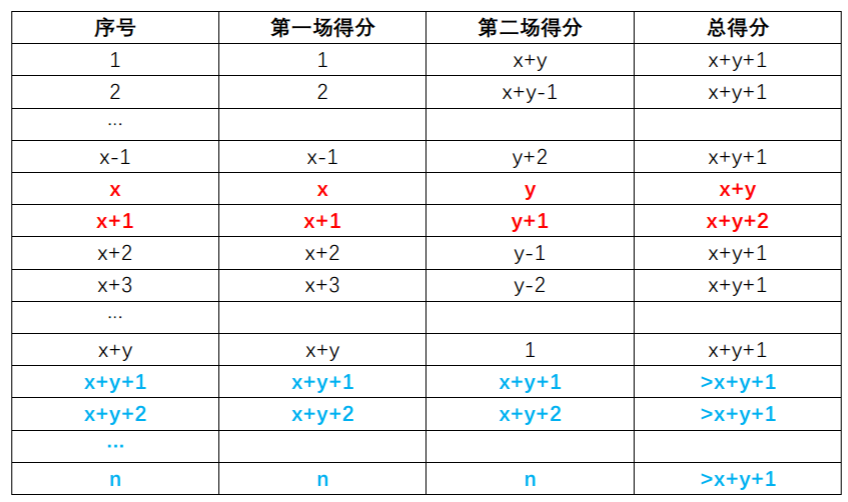
当x+y>n且y<n时,答案为x+y+1-n。
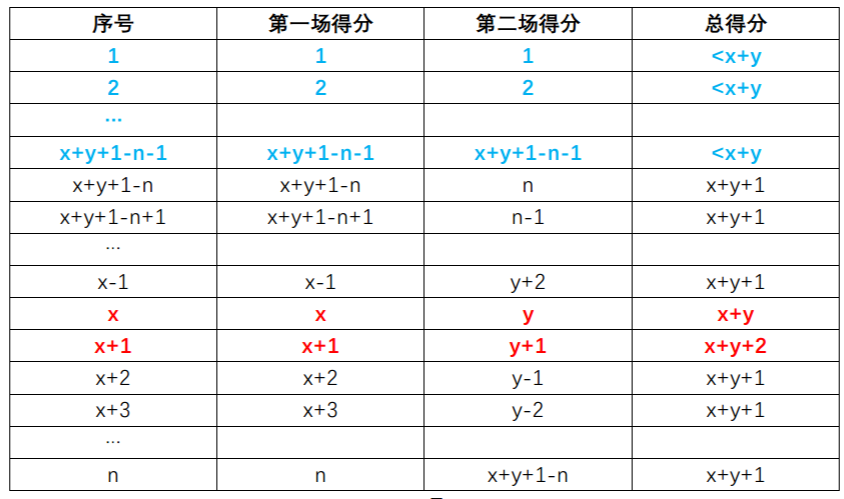
当x+y>n且y=n且x<n时,答案为x+1。
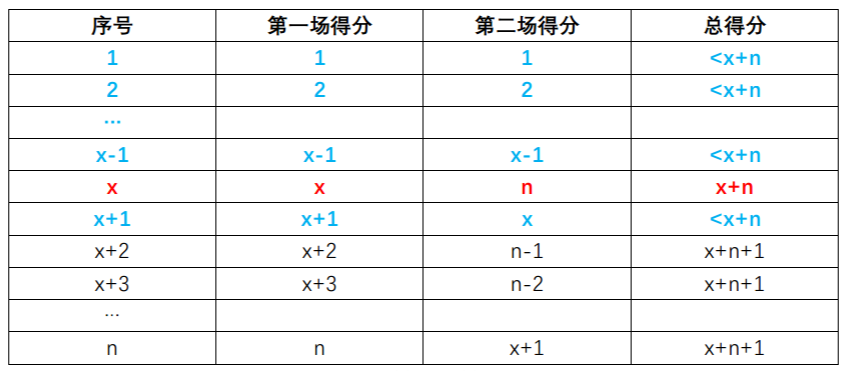
当x+y>n且y=n且x=n时,答案显然为n。
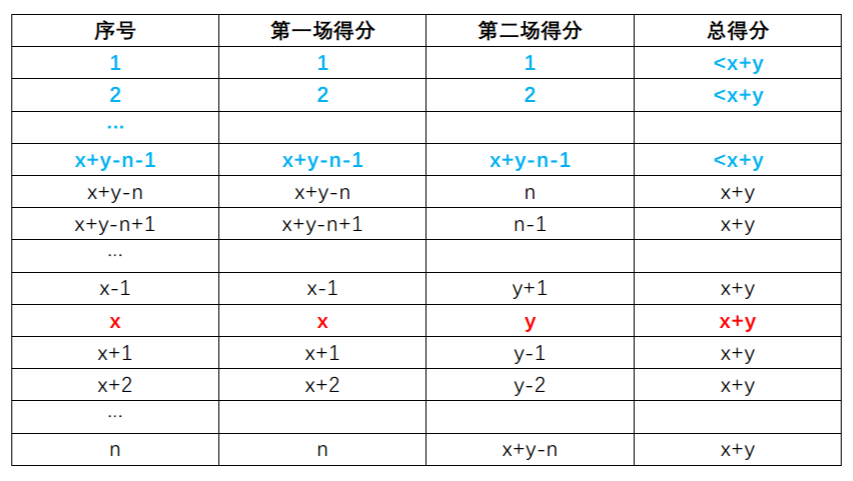
然后解决最大名次的情况,同理尽可能多构造x+y,因为得分至少要和他相等,同时又要尽可能浪费资源(减少得分比他小的人)。
当x+y-1<=n,答案为x+y-1。
当x+y-1>n,答案为n。
void test_case() {
int n, x, y;
scanf("%d%d%d", &n, &x, &y);
if(x > y)
swap(x, y);
int minans, maxans;
if(x + y <= n)
minans = 1;
else if(y < n)
minans = x + y + 1 - n;
else if(x < n)
minans = x + 1;
else
minans = n;
if(x + y - 1 <= n)
maxans = x + y - 1;
else
maxans = n;
printf("%d %d
", minans, maxans);
}
启示:要按贪心构造,尽可能节约资源或者浪费资源。要使得一段区间相等,极有可能是倒序相加,然后通过交换相邻行来微调。
C1 - Skyscrapers (easy version)
见下。
C2 - Skyscrapers (hard version)
题意:给一个n(<=5e5)个数字的数字序列,表示每个点能取到的最大值。求构造一个和最大的peak,例如:1 2 3 2 1是一个peek,10 6 6也是一个peek。准确来说,就是存在一个最高的位置,然后向两侧递减。
题解:乍一看好像做过,搞个前缀最小值和后缀最小值,但是仔细推细节的时候发现是单调栈的题,用单调栈可以维护出以某个点为结束时使得前缀部分不下降的最大值。存下前缀和后缀的最大值就可以找到那个peak的位置,然后再用一次单调栈找到peak位置时单调栈的形状,根据单调栈的形状还原出序列。
int m[500005];
int ansm[500005];
ll prefixsum[500005];
ll suffixsum[500005];
int sta[500005], top;
void test_case() {
int n;
scanf("%d", &n);
for(int i = 1; i <= n; ++i)
scanf("%d", &m[i]);
top = 0;
sta[top] = 0;
for(int i = 1; i <= n; ++i) {
while(top && m[sta[top]] >= m[i])
--top;
prefixsum[i] = prefixsum[sta[top]] + 1ll * (i - sta[top]) * m[i];
sta[++top] = i;
}
top = 0;
sta[top] = n + 1;
for(int i = n; i >= 1; --i) {
while(top && m[sta[top]] >= m[i])
--top;
suffixsum[i] = suffixsum[sta[top]] + 1ll * (sta[top] - i) * m[i];
sta[++top] = i;
}
/*for(int i = 1; i <= n; ++i)
printf("%lld%c", prefixsum[i], "
"[i == n]);
for(int i = 1; i <= n; ++i)
printf("%lld%c", suffixsum[i], "
"[i == n]);*/
top = 0;
ll ans = suffixsum[1], pos = 1;
for(int i = 1; i < n; ++i) {
ll tmp = prefixsum[i] + suffixsum[i + 1];
if(tmp > ans) {
ans = tmp;
pos = i + 1;
}
}
//printf("pos=%d
", pos);
top = 0;
for(int i = 1; i < pos; ++i) {
while(top && m[sta[top]] >= m[i])
--top;
sta[++top] = i;
}
for(int i = 1, j = 1; i < pos; ++i) {
if(j <= top && i > sta[j])
++j;
assert(j <= top);
ansm[i] = m[sta[j]];
}
top = 0;
for(int i = n; i >= pos; --i) {
while(top && m[sta[top]] >= m[i])
--top;
sta[++top] = i;
}
for(int i = n, j = 1; i >= pos; --i) {
if(j <= top && i < sta[j])
++j;
assert(j <= top);
ansm[i] = m[sta[j]];
}
for(int i = 1; i <= n; ++i)
printf("%d%c", ansm[i], "
"[i == n]);
}