简介
替罪羊树,英文名Scapegoat Tree,是一种非常暴力的平衡树,它的主要思想就是在子树不平衡的时候暴力重构子树。
操作
这里以洛谷P3369为例(https://www.luogu.com.cn/problem/P3369)。
它这道题要我们实现一下几个操作:
- 插入 x 数
- 删除 x 数(若有多个相同的数,因只删除一个)
- 查询 x 数的排名(排名定义为比当前数小的数的个数 +1 )
- 查询排名为 x 的数
- 求 x 的前驱(前驱定义为小于 x,且最大的数)
- 求 x 的后继(后继定义为大于 x,且最小的数)
定义
我们定义一个结构体数组,我们要存以下几个东西:
struct Scapegoat{
int son[2],val,Ex,Size,Fac;
}node[MAXN];
son[]:0表示左儿子,1表示右儿子
val:当前节点的值
Ex:是否真正存在在这棵树中(接下来讲到删除操作时会明白)
Size:这棵树的大小,包括被删除的点
Fac:这棵树真正的大小
由于这是动态开点,所以我们开个n[]数组记录废掉的点,以节省空间。
开点
void build(int x){
node[x].son[0]=node[x].son[1]=0;
node[x].Size=node[x].Fac=1;
}
插入
其实真的没有什么好讲的,主要是动态开点,其余的就和BST一样。
void Insert(int &nt,int x){
if(!nt){
nt=n[tot--],node[nt].val=x,node[nt].Ex=1,build(nt);//选择一个没用的点,把他插进去,然后标记为存在,再开点
return;
}
++node[nt].Size,++node[nt].Fac;//多了个节点
if(x<=node[nt].val)Insert(node[nt].son[0],x);//左子树
else Insert(node[nt].son[1],x);//右子树
}
删除
删除操作很值得一提。
替罪羊树的删除很神奇,它并不会直接删除,而是会把它标记不存在,
这时候,我们定义的Size和Fac就很有用了。如果这个点被删了,那么Fac就减1。
如果,Size值*一个固定的值Magic(我瞎取的名,一般为0.75)>Fac值,就意味着这棵树已经不平衡了,就把它重构。
void Delete(int &x,int rk)
{
if(node[x].Ex&&node[node[x].son[0]].Fac+1==rk) //如果当前节点存在且正好是我们要找的
{
node[x].Ex=0,--node[x].Fac;//删除,标记不存在,实际大小减1
return;
}
--node[x].Fac;//这个子树里有要被删除的,实际大小减1
if(node[node[x].son[0]].Fac+node[x].Ex>=rk) Delete(node[x].son[0],rk);
else Delete(node[x].son[1],rk-node[x].Ex-node[node[x].son[0]].Fac);
}
void del(int x){
Delete(rt,get_rank(x));//删除k这个数和删除k这个数的排名的数是一样的
if((double)node[rt].Size*magic>(double)node[rt].Fac) ReBuild(rt);//这棵树不平衡,要重构
}
重构
好了,终于到了最后一个操作(其实我是先学替罪羊树随笔在学主席树随笔的,不过这个替罪羊树被我咕了好久。)
重构,替罪羊树最暴力,最核心的操作。
为什么说很暴力呢?看下面就知道:
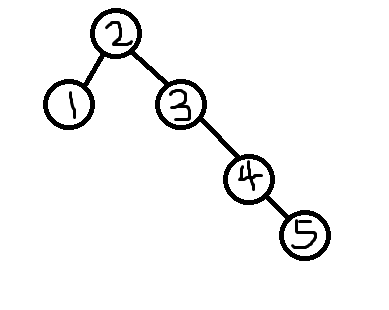
这是一颗BST树,很明显地看出,这极其不平衡,唯一比它更不平衡的只有一条链了。

我们先把它按照中序遍历压扁,变成上面那样。
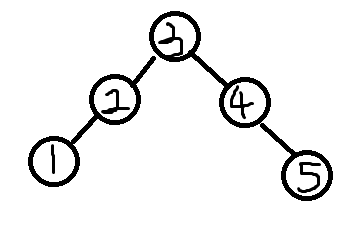
我们再把它提起来,就像上面那样,是不是so easy!
附上代码:
void balala(int x){//给爷变扁
if(!x)return;
balala(node[x].son[0]);//先变扁左子树,中序遍历
if(node[x].Ex)cur[++cnt]=x;//再本人,如果存在的话
else n[++tot]=x;//如果不存在就当不存在,再留着这个位置下次用
balala(node[x].son[1]);//右子树
}
void PickUP(int l,int r,int &x){
int mid=l+r>>1;x=cur[mid];
if(l==r){
build(x);//开点
return;
}
PickUP(l,mid-1,node[x].son[0]);
PickUP(mid+1,r,node[x].son[1]);//在提左右子树
PushUp(x);//再重建大小。
}
void ReBuild(int &x)
{
cnt=0,balala(x);//拍扁
if(cnt)PickUP(1,cnt,x);//重建
else x=0;
}
代码
#include<bits/stdc++.h>
using namespace std;
const int MAXN=100005;
const int magic=0.75;
struct Scapegoat{
int son[2],val,Ex,Size,Fac;
}node[MAXN];
int N;
int opt,x,st;
int n[MAXN],cur[MAXN];
int rt,tot,cnt;
void build(int x){
node[x].son[0]=node[x].son[1]=0;
node[x].Size=node[x].Fac=1;
}
bool balance(int x)
{
return (double)node[x].Fac*magic>(double)max(node[node[x].son[0]].Fac,node[node[x].son[1]].Fac);
}
void Insert(int &nt,int x){
if(!nt){
nt=n[tot--],node[nt].val=x,node[nt].Ex=1,build(nt);
return;
}
++node[nt].Size,++node[nt].Fac;
if(x<=node[nt].val)Insert(node[nt].son[0],x);
else Insert(node[nt].son[1],x);
}
void balala(int x){
if(!x)return;
balala(node[x].son[0]);
if(node[x].Ex)cur[++cnt]=x;
else n[++tot]=x;
balala(node[x].son[1]);
}
void PushUp(int x)
{
node[x].Size=node[node[x].son[0]].Size+node[node[x].son[1]].Size+1,node[x].Fac=node[node[x].son[0]].Fac+node[node[x].son[1]].Fac+1;
}
void PickUP(int l,int r,int &x){
int mid=l+r>>1;x=cur[mid];
if(l==r){
build(x);
return;
}
if(l<mid)PickUP(l,mid-1,node[x].son[0]);
else node[x].son[0]=0;
PickUP(mid+1,r,node[x].son[1]);
PushUp(x);
}
void ReBuild(int &x)
{
cnt=0,balala(x);
if(cnt)PickUP(1,cnt,x);
else x=0;
}
void check(int nt,int x){
int s=x<=node[nt].val?0:1;
while(node[nt].son[s])
{
if(!balance(node[x].son[s]))
{
ReBuild(node[x].son[s]);
return;
}
x=node[x].son[s],s=x<=node[x].val?0:1;
}
}
int get_rank(int v)
{
int x=rt,rk=1;
while(x)
{
if(node[x].val>=v) x=node[x].son[0];
else rk+=node[node[x].son[0]].Fac+node[x].Ex,x=node[x].son[1];
}
return rk;
}
int get_val(int rk)
{
int x=rt;
while(x)
{
if(node[x].Ex&&node[node[x].son[0]].Fac+1==rk) return node[x].val;
else if(node[node[x].son[0]].Fac>=rk) x=node[x].son[0];
else rk-=node[x].Ex+node[node[x].son[0]].Fac,x=node[x].son[1];
}
}
void Delete(int &x,int rk)
{
if(node[x].Ex&&node[node[x].son[0]].Fac+1==rk)
{
node[x].Ex=0,--node[x].Fac;
return;
}
--node[x].Fac;
if(node[node[x].son[0]].Fac+node[x].Ex>=rk) Delete(node[x].son[0],rk);
else Delete(node[x].son[1],rk-node[x].Ex-node[node[x].son[0]].Fac);
}
void del(int x){
Delete(rt,get_rank(x));
if((double)node[rt].Size*magic>(double)node[rt].Fac) ReBuild(rt);
}
int main(){
cin >> N;
tot=0;
for(int i=N-1;i;--i)n[++tot]=i;
for(int i=1;i<=N;i++){
cin >> opt >> x;
if(opt==1){
Insert(rt,x);
check(st,x);
}
if(opt==2){
del(x);
}
if(opt==3){
cout << get_rank(x) << endl;
}
if(opt==4){
cout << get_val(x) << endl;
}
if(opt==5){
cout << get_val(get_rank(x)-1) << endl;
}
if(opt==6){
cout << get_val(get_rank(x+1)) << endl;
}
}
return 0;
}