递归定义的算法有两部分:
递归基:直接定义最简单情况下的函数值;
递归步:通过较为简单情况下的函数值定义一般情况下的函数值。
应用条件与准则:
(1)问题具有某种可借用的类同自身的子问题描述的性质;
(2)某一问题有限步的子问题(也称做本原问题)有直接的解存在。
在计算机中是利用栈来实现recursion的,对于每一次递归的调用,计算机都会将调用者的局部变量以及返回地址储存在栈中,待回调时恢复局部变量,并返回到调用地址中
正因计算机会保存所有的局部变量,这将导致额外的开销,使程序运行效率底下,我们可以拿计算斐波那契数列作例子
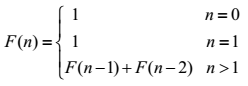
由此形式读者很容易想到用递归解决问题,但这往往是一个陷进
当n!=0||n!=0时,我们将要执行 ,在F(n-1)中又要执行F(n-2)+F(n-3),在F(n-2)中执行F(n-3)+F(n-4),要掉用以及保存的变量数量呈级数式的增长,同时其中又存在许多重复的,这么做个程序带来了额外的开销,显得recursion效率低下
,在F(n-1)中又要执行F(n-2)+F(n-3),在F(n-2)中执行F(n-3)+F(n-4),要掉用以及保存的变量数量呈级数式的增长,同时其中又存在许多重复的,这么做个程序带来了额外的开销,显得recursion效率低下
下面我们来具体比较一下
#include<iostream>
#include<ctime>
using namespace std;
//递归
int recursion(int n)
{
if(n==1||n==2)
return 1;
else
return recursion(n-1)+resursion(n-2);
}
//迭代
int iteration(int n)
{
int p1=1;
int p2=1;
while(n->2)
{
int temp=p2;
p2=p1+p2;
p1=temp;
}
return p2;
}
int main()
{
int n;
cin>>n;
clock_t start=clock();
recursion(n);
clock_t end=clock();
cout<<"Recursion 用时: "<< start-end << endl;
start=clock();
iteration(n);
end=clock();
cout<<"iteration 用时: "<< start-end << endl;
return 0;
}