3.3 Histogram Processing

\(r_k\)表示一个\(L\)级的图像\(f(x,y)\)，\(f\)的未标准化直方图表示为：

\[h(r_k)=n_k \]

\(n_k\)表示\(f\)中强度为\(r_k\)的像素点数量。标准化的直方图定义为：

\[p(r_k)=\frac{h(r_k)}{MN}=\frac{n_k}{MN} \]

\(M\)、\(N\)为图像的长宽像素点数。

直方图均衡 Histogram Equalization

• \(r\)：将要被处理的灰度值，\(r\in[0,L-1]\)，\(r=0\)表示为黑，\(255\)为白；

• \(s\)：处理后的灰度值，由以下映射关系得出：

\[s=T(r) \]

​ 上述关系满足两个条件：

1. \(T(r)\)是单调递增函数；
2. \(0\leq T(r)\leq L-1\)，当\(0\leq r \leq L-1\)。

但是有时候会用到逆映射：

\[r=T^{-1}(s) \]

这时候如果\(T(r)\)还是单调函数，就会导致出现一对多的情况。所以\(T(r)\)应该是一个严格的单调递增函数。

两个定义域存在映射关系的随机变量概率密度函数之间的关系

令\(p_r(r)\)，\(p_s(s)\)代表在两张不同图像（均衡前与均衡后，使用函数\(T(r)\)进行均衡）中，随机变量\(r\)与\(s\)的PDF（概率密度函数）。根据\(T(r)=s\)且\(p_r(r)\)已知，我们有如下关系：

\[p_s(s)=p_r(r)\left |{\frac {dr}{ds}}\right | \]

通过上式我们可以得出结论：输出灰度变量\(s\)的PDF由输入图像的PDF与映射关系\(s=T(r)\)决定。

上述结论可以抽象为：我们目前已知映射关系$y=g(x) \(并且\)y\(单调递增（递减），\)x=g^{-1}(y)\(为其反函数；已知\)f(x)\(。并且\)f_y(y)=p(y)\(,\)f_x(x)=p(x)\(。\)F_Y(y)=P(Y\leq y)\(,\)F_X(x)=P(X\leq x)\(。求\)f(y)$。

证：\((1)\)首先证明单调递增的情况。

\[F_Y(y)=P(Y\leq y)=P(g(x)\leq y)=P[x\leq g^{-1}(y)]=F_x[g^{-1}(y)] \]

上式两边求导，得

\[f_Y(y)=f_x[g^{-1}(y)]\times {(g^{-1})}^{'}(y)=f_X(x)\times \frac{dx}{dy}\\ \frac{f_Y(y)}{f_X(x)}=\frac{dx}{dy} \]

\((2)\)​单调递减

\[F_Y(y)=P(Y\leq y)=P(g(x)\leq y)=1-P[x\leq g^{-1}(y)]=1-F_x[g^{-1}(y)] \]

求导，得

\[f_Y(y)=-f_x[g^{-1}(y)]\times {(g^{-1})}^{'}(y)=-f_X(x)\times \frac{dx}{dy}\\ \frac{f_Y(y)}{f_X(x)}=\left |{\frac{dx}{dy}} \right | \]

即为式\((5)\).

连续图像通用直方图均衡公式及其属性

图像处理中的一个重要函数为：

\[s=T(r)=(L-1)\int_0^r p_r(w)dw \]

连续图像直方图均衡后图像的概率密度

由公式\((5)\)我们可以得到：

\[\begin{align} \frac{ds}{dr}&=\frac{dT(r)}{dr}\nonumber \\ &=(L-1)\frac{d}{dr}\left[ \int _0^rp_r(w)dw \right]\nonumber \\ &=(L-1)p_r(r) \end{align} \]

用公式\((11)\)替代\((5)\)得到

\[\begin{align}p_s(s)&=p_r(r）\left| {\frac{dr}{ds}}\right |\nonumber \\ &=p_r(r)\left | {\frac{1}{(L-1)p_r(r)}}\right |\nonumber \\ &=\frac{1}{L-1}\ \ \ \ 0\leq s \leq L-1 \end{align} \]

从公式\((12)\)可以看出，这是一个均匀概率密度函数，也就证明\((10)\)的变换可以得到一个随机变量\(s\)，\(s\)可以用均匀PDF表征。也就是说，无论初始的\(p_r(r)\)如何，经过s=T(r)变换后，得到的\(p_s(s)\)始终是均匀的，与\(p_r(r)\)无关。

上面讨论的都是连续函数，对于离散值来说，有以下关系：

\[s_k=T(r_k)=(L-1)\sum_{j=0}^{k}p_r(r_j)\ \ k=0,1,2\dots L-1 \]

下面是一个例子：

假设图像是\(3bits\)灰度级（\(L=8\)），大小为\(64*64(MN=4096)\)，灰度值分布如下表：

\(r_k\)	n_k	\(p_r(r_k)=n_k/MN\)
\(r_0=0\)	790	0.19
\(r_1=1\)	1023	0.25
\(r_2=2\)	850	0.21
\(r_3=3\)	656	0.16
\(r_4=4\)	329	0.08
\(r_5=5\)	245	0.06
\(r_6=6\)	122	0.03
\(r_7=7\)	81	0.02

经过\((13)\)映射后的值可以用像下面的方法得到：

\[s_0=T(r_0)=7\sum_{j=0}^0 p_r(r_j)=7p_r(r_0)=1.33 \]

对每个值进行四舍五入之后：

\(s_0=1.33\rightarrow 1\)，\(s_1=3.08\rightarrow 3\)，\(s_2=4.55\rightarrow 5\)，\(s_3=5.67\rightarrow 6\)，\(s_4=6.23\rightarrow 6\)，

\(s_5=6.65\rightarrow 7\)，\(s_6=6.86\rightarrow 7\)，\(s_7=7.00\rightarrow 7\)

也就是说，原本图像有8中灰度值，经过均衡后，图像只有5中灰度值了。对于灰度值7，有\((245+122+81)=448\)个像素点。

由于我们刚才取得是PDF的近似值，而且没有创建新的灰度级别，所以刚才的均衡化并不完美。

直方图匹配（规定化）Histogram Matching(Specification)

直方图匹配（Histogram Matching ），又称为直方图规定化（Histogram Specification），是指在处理图像时，由处理人员通过PDF函数，指定输出图像的直方图形状。

首先令

\[s=T(r)=(L-1)\int_0^rp_r(w)dw \]

也就是说，如果一张图片灰度值为\(r\)，经过\(T\)变换，可以得到均衡的图片\(s\)。

假设对于输入图像，存在另一个灰度值集合为\(z\)​的图像，该图像与原图像内容相同，只是灰度值不同。

\(z\)经过变换\(G\)，可以有如下关系：

\[G(z)=(L-1)\int_0^zp_z(v)dv=s \]

\(r\)经过变换得到了\(s\)，\(z\)经过变换也得到了\(s\)。也就是说，两幅灰度值不同的图像可以经过均衡后的图像这一桥梁建立连接。\(z\)与\(r\)的关系如下：

\[z=G^{-1}(s)=G^{-1}[T(r)] \]

这就是说，两副内容相同灰度值不同的图像，可以很方便地找到两副图像的灰度映射关系。这也就是为什么该灰度变换被称为直方图匹配或直方图规定化的原因，它们的目的就是给定两副相同内容不同灰度分布图像，通过这两副图像本身的灰度概率密度函数就可以找到二者的映射关系。

连续灰度直方图的处理步骤

1. 首先获取图片的\(p_r(r)\)；
2. 通过\((16)\)得到\(G(z)\);
3. 计算逆变换\(z=g^{-1}(s)\)，就可以得到输出图像的灰度值\(z\)。

但是经过这种处理后的值不能直接使用，还需要进行离散处理。在实际中并不需要计算G的倒数，因为实际中的像素值都是整数，只需要将数值进行四舍五入，然后存储在表中。然后当给定一个值\(s\)时，进行查表寻找最接近的值。

数字图像直方图均衡化处理的步骤

1. 计算给定图像的直方图\(p_r(r)\)，使用\(s=T(r)=(L-1)\int_0^rp_r(w)dw\)来计算输入图像到均衡图的映射关系\(s_k\)，对计算结果进行四舍五入处理；
2. 使用\(G(z)=(L-1)\int_0^zp_z(v)dv=s\)计算\(G(z)\)的所有可能值\(z_q\)。其中\(p_z(z)\)是规定的图像直方图的值，并进行四舍五入，最后将结果存储在一张表中。

​ 到目前为止，我们得到了：输入图像\(r\)到均衡后的图像\(s\)的映射关系、规定的图像\(z\)到均衡后的图像s的映射关系，且这个映射关系存在了表中。

3. 对于每一个\(s_k\)，使用2中存储的值查表，让\(G(z_q)\)最接近\(s_k\)。当有多个值满足条件时（也就是映射不唯一），选取最小值。
4. 使用步骤 3 找到的映射把该图像中的每个均衡后的像素值\(s_k\)映射为直方图规定化后的图像中的相应\(z_q\)值，形成直方图规定化后的图像。

与连续情况相比，离散情况少了很多中间步骤，不需要计算\(G^{-1}\).

例子：

输入图像大小\(MN=4096\)，色深\(3bit(L=8)\)。灰度分布与直方图值如下：

\(r_k\)	\(n_k\)	\(p_r(r_k)=n_k/MN\)
\(r_0=0\)	790	0.19
\(r_1=1\)	1023	0.25
\(r_2=2\)	850	0.21
\(r_3=3\)	656	0.16
\(r_4=4\)	329	0.08
\(r_5=5\)	245	0.06
\(r_6=6\)	122	0.03
\(r_7=7\)	81	0.02

现在要变换这个直方图，让其有下表中第二列的值：

\(z_q\)	指定的\(p_z(z_q)\)	实际的\(p_z(z_q)\)
\(z_0=0\)	\(0.00\)	\(0.00\)
\(z_1=1\)	\(0.00\)	\(0.00\)
\(z_2=2\)	\(0.00\)	\(0.00\)
\(z_3=3\)	\(0.15\)	0.19
\(z_4=4\)	0.20	0.25
\(z_5=5\)	0.30	0.21
\(z_6=6\)	0.20	0.24
\(z_7=7\)	0.15	0.11

第一步：对第一个表中的原图进行直方图均衡，求出\(s_k\)的值（使用\(s=T(r)=(L-1)\int_0^rp_r(w)dw\)）：

​ \(s_0=1.33\rightarrow 1\)，\(s_1=3.08\rightarrow 3\)，\(s_2=4.55\rightarrow 5\)，\(s_3=5.67\rightarrow 6\)，\(s_4=6.23\rightarrow 6\)，

​ \(s_5=6.65\rightarrow 7\)，\(s_6=6.86\rightarrow 7\)，\(s_7=7.00\rightarrow 7\)

​ 第二个表中的第三列就是上面进过均衡后的\(p_z\)。

第二步：计算第二个表中第二列的值，也就是规定的直方图与均衡后的直方图之间的映射关系。

\(G(z_0)=0.00\rightarrow 0\)，\(G(z_1)=0.00\rightarrow 0\),\(G(z_2)=0.00\rightarrow 0\)，\(G(z_3)=1.05\rightarrow 1\)

\(G(z_4)=2.45\rightarrow 2\)，\(G(z_5)=4.55\rightarrow 5\)，\(G(z_6)=5.95\rightarrow 6\)，\(G(z_7)=7.00\rightarrow 7\)

也就是\(G(z_q)\)与\(z_q\)之间的映射关系：

\(z_q\)	\(G(z_q)\)
\(z_0\)	0
\(z_1\)	0
\(z_2\)	0
\(z_3\)	1
\(z_4\)	2
\(z_5\)	5
\(z_6\)	6
\(z_7\)	7

然后查表，找到对应关系：

\(s_k\)	\(z_q\)
1	3
3	4
5	5
6	6
7	7

精确直方图匹配Exact Histogram Matching(Specification)

上面的两种方法：直方图均衡与规格化并不能产生精确形状的直方图。因为在进行均衡化的时候，像素有四舍五入，有一些像素就被丢弃了；在查表时，有一些像素的数量发生了变化。这两种情况导致直方图在y轴发生了一定的偏移。下面介绍的方法可以让直方图有指定的形状。

首先指定一个我们直方图，这个直方图是我们需要让图像最后变换到的。

\[H=\{ h(0),h(1),h(2),\dots,h(L-1)\} \]

其中\(h(j)\)是灰度为\(j\)的像素数量。假设此直方图未标准化，且是一个有效的直方图：

\[\sum_{j=0}^{L-1}h(j)=MN \]

对于以上直方图，进行如下步骤：

1. 根据预定义的标准，对图像像素进行排序；
2. 将有序的像素划分为\(L\)组，第\(j\)组有\(h\)(j)个像素；
3. 将灰度\(j\)指定给第\(j\)组中的所有像素。

排序

我们对每个像素点定义以下严格偏序关系：

\[f(x_0,y_0)<f(x_1,y_1)<\dots<f(x_{M-1,N-1},y_{M-1,N-1}) \]

但是对于绝大多数图像来说，像素点的个数远远大于灰度值的最大值。所以我们使用一个点的邻域中所有像素灰度值的平均值来进行排序。

\(W_k\)代表的是一个点的邻域集合。每一个不同的k代表一个不同的kernel。

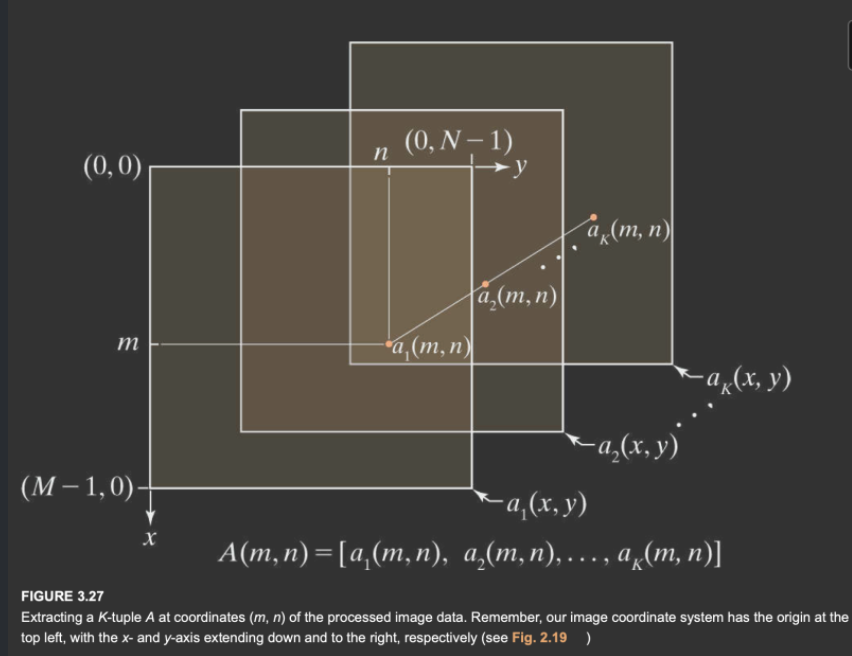
对于一个点\((x,y)\)，\(a_k(x,y)\)代表在\(W_k\)中(x,y)点的平均值。\(A(x,y)\)表示在\(K\)邻域中灰度平均值形成的\(K\)元组。

\[A(x,y)=[a_1(x,y),a_2(x,y),\dots,a_k(x,y)] \]

因为平均操作应用于了每个像素，所以对K元组进行排序相当于对元素进行排序。

对于K的选取，应该尽可能小，因为K较小的话，重复也就越少，中心点与其邻域的关联也就越大。

计算邻域平均值与提取K元组

选取K个kernel，使用这K个kernel对图片进行平均操作，最后得到K个矩阵。

精确直方图规格化算法

给定一张图片\(f(x,y)\)，大小\(M\times N\)，有\(L\)个灰度级：

1. 指定直方图\(H=\{h(0),h(1),\dots,h(L-1)\}\)；
2. 指定\(K\)的值；
3. 使用上面的K来生成K个图片：\(a_1(x,y),a_2(x,y),\dots,a_K(x,y)\)；
4. 使用基于列的线性索引进行扫描，从处理后的图像中提取出(21)形式的\(MN\)个\(K\)元组，这时每个\(K\)元组都与同一层中，相同坐标的像素相关联。K元组与和它相关的元素的顺序由线性索引\(\alpha=[0,1,2 \dots ,MN-1]\)给出。

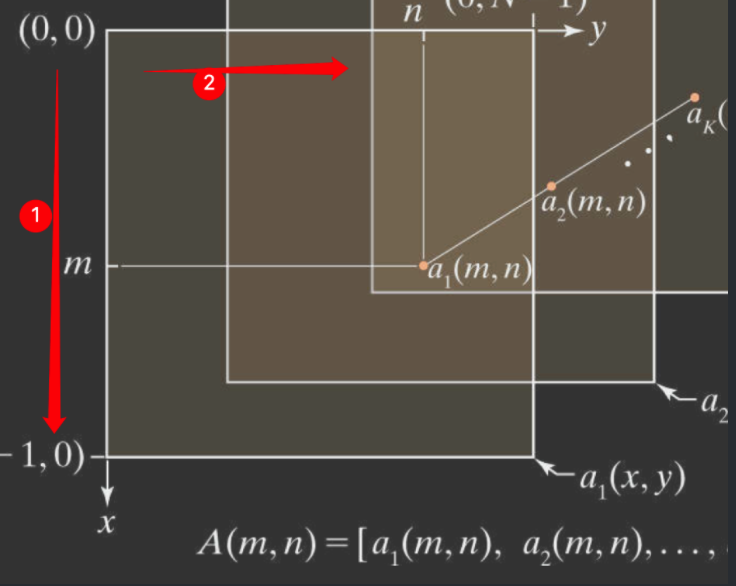
线性索引：观察上图，这是一个\(M\times N\times K\)的矩阵。线性扫描时，从上到下，从左到右。对每个点进行索引，每个点的索引有如下关系：

\[\alpha=My+x \]

5. 根据上一步的结果，生成一个大小为\(MN\times K\)的矩阵\(Q\)，根据\(\alpha\)排序。这种构造方式保留了每个\(K\)元组与其对应的像素之间的关系。Q的形式如下：

   \[\begin{pmatrix} a_1(0,0)&a_2(0,0)&\cdots& a_k(0,0)\\ a_1(1,0)&a_2(1,0)&\cdots& a_k(1,0)\\ \vdots &\vdots &\ddots&\vdots\\ a_1(x,y)&a_2(x,y)&\cdots& a_k(x,y) \end{pmatrix} \]

   从上到下，每一行的顺序是上面的\(\alpha\)。

6. 按照升序对\(Q\)行进行字典序排列。并用一个字符串\(O\)来表示这个顺序。比如如果将\(Q\)的第28行移动到了第0行，则O的第一个元素为28.

如果\(a_1(t,v)<a_1(w,z)\)，或者\(a_i(t,v)=a_i(w,z),a_j(t,x)<a_j(w,z)\)，则称A(w,z)按照字典序排序。

5. 从第一个元素开始，将字符串\(O\)的\(MN\)个元素分成\(L\)组，让第\(j\)组有\(h(j)\)个元素。

6. 将\(h(j)\)组中的所有元素的灰度值赋值为\(j,j=0,1\cdots L-1\)。这就为O的每一个元素指定了一个强度值，生成了一对\(\{O,I\}\)，\(I\)也是一个字符串，长度与$$O相同，包含着分配给\(O\)元素的相应的强度值。

7. 构造输出图像。\(\{O,I\}\)中包含了一个线性索引值，根据这个索引值我们就能将这个点还原到图象上：

   \[x=o\ mod\ M\\ y=(o-x)/M \]

   \(I\)就是该点的强度值。

精确直方图均衡会出现的问题与解决方法

对于一般的图像来说，这种方法可以很好地均衡图像。但是如果图象中出现了大量的、具有相同灰度值的像素，精确直方图均衡就无法处理了。

一种解决方法是将这些无法处理的区域使用遮罩遮起来，对剩余部分进行均衡。

局部直方图处理 Local Histogram Processing

目前为止介绍过的图像处理方法都是对整张图片操作的，对于图像中的一些小细节上的处理可能并不尽如人意。下面介绍的方法是对图片进行局部处理。

该方法同样是定义一个邻域，并在水平与垂直方向上移动kernel。因为在邻域的移动过程中，每次只有一行或者一列会发生变化，所以说我们可以用本次移动时获得的新数据来更新上一次的数据，然后生成直方图。这样就减少了移动时的计算开销。

直方图统计在图像增强中的应用

• \(r\)：表示在\([0,L-1]\)范围内的离散值。

• \(p(r_i)\)表示对应于灰度\(r_i\)的归一化直方图分量，也就是直方图中\(r_i\)出现的概率。

• n阶矩：

\[\mu _n=\sum_{i=0}^{L-1}(r_i-m)^np(r_i) \]

​ m为期望值（平均值）：

\[m=\sum_{i=0}^{L-1}r_ip(r_i) \]

平均值是平均灰度值的度量。

而方差，或者标准差\(\sigma\)：

\[\sigma^2=\mu_2=\sum_{i=0}^{L-1}(r_i-m)^2p(r_i) \]

是图片的对比度的度量。

（26）与（27）都是在整张图片上计算的。在用作局部增强时，平均值与方差是更有作用的参数。

\((x,y)\)是图片中的任意像素，\(S_{xy}\)表示以\((x,y)\)为中心的邻域。在这个邻域上的平均值由下式给出：

\[m_{s_{xy}}=\sum_{i=0}^{L-1}r_ip_{s_{xy}}(r_i) \]

\(p_{s_{xy}}\)是在区域\(s_{xy}\)像素的直方图。直方图有L个单元，对应于\(L\)个在输入图像中可能出现的灰度值。但是许多的单元都会是\(0\)值。比如说一个\(3\times 3\)的邻域，\(L=256\)。在这个邻域上，只可能出现\(1\sim9\)种灰度值。

在邻域中的方差由下式给出：

\[\sigma^2_{s_{xy}}=\sum_{i=0}^{L-1}(r_i-m_{s_{xy}})^2p_{s_{xy}}(r_i) \]

和全局一样，局部平均值是邻域中平均强度的度量，而局部方差（标准差）是邻域中灰度的对比值的度量。

我们需要在图片中进行均衡的，是相对于其他区域来说，对比度较低的部分。可以用下面的方法来判断一个区域是否需要进行均衡：

首先判断一个区域相对来说是否较暗或者较亮：

\[k_0m_G \leq m_{s_{xy}}\leq k_1m_G \]

\(k_0,k_1\)是非负整数，并且\(k_0 \leq k_1\)。比如我们想关注一个区域，这个区域较于整张图的\(1/4\)区域更暗，我们可以选取\(k_0=0,k_1=0.25\)。

判断一个区域的对比度是否较低：

\[k_2\sigma _G \leq \sigma_{s_{xy}}\leq k_3\sigma_G \]

\(k_2,k_3\)是非负整数，并且\(k_0 \leq k_1\)。比如我们想关注一个区域，这个区域比较暗并且对比度较低，我们可以选取\(k_2=0,k_3=0.1\)。通过将上式同时乘一个常数\(C\)，就可以改变其相对于图像其他部分的对比度。并且不符合条件的像素不会发生改变。

将上面的方法总结如下：

用f(x,y)来代表在点(x,y)上的灰度值，集合g(x,y)表示相应像素增强后的值。

\[g(x,y)=\left \{ \begin{array}{**lr**} Cf(x,y)\ \ 如果k_0 \leq m_{s_{xy}}\leq k_1m_G且k_2\sigma_G\leq \sigma_{s_{xy}}\leq k_3\sigma_G,& \\ f(x,y)\ \ 其他情况& \end{array} \right. \]

\(x=0,1,2\dots,M-1,y=0,1,2,\dots,N-1\)，\(m_G\)是输入图像的全局平均值，\(\sigma_G\)是标准差。\(m_{s_{xy}}\)是局部平均值，\(\sigma_{s_{xy}}\)是局部标准差。