机器学习是时下流行AI技术中一个很重要的方向,无论是有监督学习还是无监督学习都使用各种“度量”来得到不同样本数据的差异度或者不同样本数据的相似度。良好的“度量”可以显著提高算法的分类或预测的准确率,本文中将介绍机器学习中各种“度量”,“度量”主要由两种,分别为距离、相似度和相关系数,距离的研究主体一般是线性空间中点;而相似度研究主体是线性空间中向量;相关系数研究主体主要是分布数据。本文主要介绍相似度。
1 Jaccard相似度——集合论的妙用
Jaccard相似度,或者叫做并交比。是用于比较样本集的相似性与多样性的统计量。雅卡尔系数能够量度有限样本集合的相似度,其定义为两个集合交集大小与并集大小之间的比例:
设A和B是两个集合,则A和B的Jaccard相似度为:
若集合A和B完全一样则定义J(A,B)=1,显示0<=J(A,B)<=1
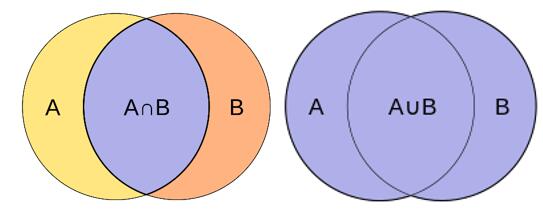
图1 集合A和集合B的交集和并集
下面通过简单例子来说明Jaccard相似度如何计算的,设
集合A = {“A”,“B”, “C”,“D“}
集合B = {“A”,“B”, “E”,F“, “G”}
A和B的并集A∪B = {“A”,“B”, “C”,“D“, “E”,“F”, “G”}
A和B的交集A∩B = {“A”, “B” }
所以|A∪B| = 7, | A∩B| =2
所以A和B的Jaccard相似度为2/7
2 余弦相似度——NLP领域大杀器
余弦相似度通过测量两个向量内积空间的夹角的余弦值来度量它们之间的相似性。0度角的余弦值是1,而其他任何角度的余弦值都不大于1。用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量,也就是衡量两个向量在方向上的差别。
如果向量a = (a1, a2,..., an) 和向量b = (b1, b2, ..., bn) 是两个欧式空间点,则两向量的点积为a⋅b=|a|⋅|b|⋅cos⟨a,b⟩,向量都是有方向的量,cos⟨a,b⟩就是a和b夹角的余弦,所以两个向量a和b的余弦相似度计算公式为:
比如向量x=(0,1,2)和y=(1,0,2),那么它们余弦距离为
余弦相似度通常用于信息检索中。在信息检索领域中,每个词条拥有不同的度,一个文档是由一个由有权值的特征向量表示的,权值的计算取决于词条在该文档中出现的频率。余弦相似度因此可以给出两篇文档其主题方面的相似度。另外,它通常用于文本挖掘中的文件比较。此外,在数据挖掘领域中,用它来衡量集群内部的凝聚力。