Knight Moves
Description
A friend of you is doing research on the Traveling Knight Problem (TKP) where you are to find the shortest closed tour of knight moves that visits each square of a given set of n squares on a chessboard exactly once. He thinks that the most difficult part of the problem is determining the smallest number of knight moves between two given squares and that, once you have accomplished this, finding the tour would be easy.
Of course you know that it is vice versa. So you offer him to write a program that solves the "difficult" part.
Your job is to write a program that takes two squares a and b as input and then determines the number of knight moves on a shortest route from a to b.
Input
The input file will contain one or more test cases. Each test case consists of one line containing two squares separated by one space. A square is a string consisting of a letter (a-h) representing the column and a digit (1-8) representing the row on the chessboard.
Output
For each test case, print one line saying "To get from xx to yy takes n knight moves.".
Examples
Input
e2 e4
a1 b2
b2 c3
a1 h8
a1 h7
h8 a1
b1 c3
f6 f6
Output
To get from e2 to e4 takes 2 knight moves.
To get from a1 to b2 takes 4 knight moves.
To get from b2 to c3 takes 2 knight moves.
To get from a1 to h8 takes 6 knight moves.
To get from a1 to h7 takes 5 knight moves.
To get from h8 to a1 takes 6 knight moves.
To get from b1 to c3 takes 1 knight moves.
To get from f6 to f6 takes 0 knight moves.
描述:
在一个8×8的方格棋盘中,按照国际象棋中马的行走规则从棋盘上的某一方格出发,开始在棋盘上周游
当骑士走到给定的终点时,最短的路程是多少。
正确解法:
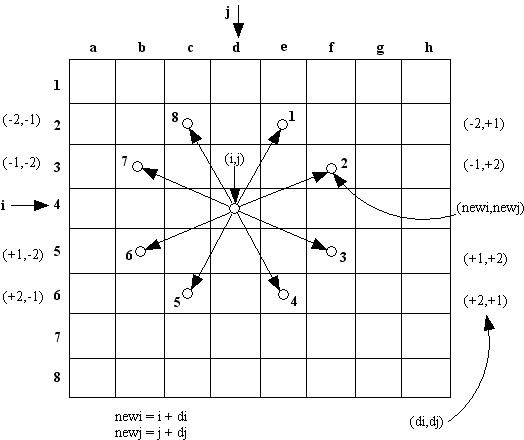
骑士有八个走的方向。
(经典的bfs)记录一下认真写bfs的我。

1 #include<iostream> 2 #include<cstdio> 3 #include<string> 4 #include<cstring> 5 #include<algorithm> 6 #include<cmath> 7 using namespace std; 8 char aa[5], bb[5]; 9 int book[10][10] = { 0 }; 10 int next1[10][2] = { {-2,-1},{-1,-2},{1,-2},{2,-1}, 11 {-2,1},{-1,2},{1,2},{2,1} }; 12 struct student 13 { 14 int x, y, step; 15 }que[110]; 16 int bfs(int x1,int x2,int x3,int x4) 17 { 18 int ans = 0; 19 int head = 1, tail = 2; 20 bool flag = 0; 21 que[head].x = x1; 22 que[head].y = x2; 23 que[head].step = 0; 24 book[x1][x2] = 1; 25 while (head < tail) 26 { 27 for (int k = 0; k <= 7; k++) 28 { 29 int tx = que[head].x + next1[k][0]; 30 int ty = que[head].y + next1[k][1]; 31 if (tx > 0 && tx < 9 && ty>0 && ty < 9 && book[tx][ty] == 0) 32 { 33 book[tx][ty] = 1; 34 que[tail].x = tx; 35 que[tail].y = ty; 36 que[tail].step = que[head].step + 1; 37 tail++; 38 } 39 if (tx == x3 && ty == x4) 40 { 41 flag = 1; 42 break; 43 } 44 } 45 if (flag == 1) 46 { 47 ans = que[tail - 1].step; 48 return ans; 49 } 50 head++;; 51 } 52 } 53 54 int main() 55 { 56 while (cin >> aa >> bb) 57 { 58 memset(que, 0, sizeof(que)); 59 memset(book, 0, sizeof(book)); 60 int x1 = aa[0] - 'a' + 1; 61 int x2 = aa[1] - '0'; 62 int x3 = bb[0] - 'a' + 1; 63 int x4 = bb[1] - '0'; 64 if (x1 == x3 && x2 == x4) 65 printf("To get from %s to %s takes 0 knight moves. ",aa,bb); 66 else { 67 int aaa=bfs(x1, x2, x3, x4); 68 printf("To get from %s to %s takes %d knight moves. ",aa,bb,aaa); 69 } 70 } 71 return 0; 72 }
