主成分分析法(PAC)的优化——选择主成分的数量
根据上一讲,我们知道协方差为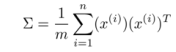 ①
①
而训练集的方差为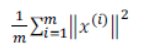 ②。
②。
我们希望在方差尽可能小的情况下选择尽可能小的K值。
也就是说我们需要找到k值使得①/②的值尽可能小(≤0.01)
那么我们可以先令K = 1 然后进行主要成分分析,得到U reduce 和 Z 计算其比例是否小鱼0.01,如果不是就令K = 2 再进行计算。
直到找到使得比例满足的k的最小值。
不过,在octave中,我们也利用在调用svd函数时候,得到的 S,U ,V参数进行判断。S是一个n×n的对角矩阵,它的元素都在左对角线上。因此可以计算
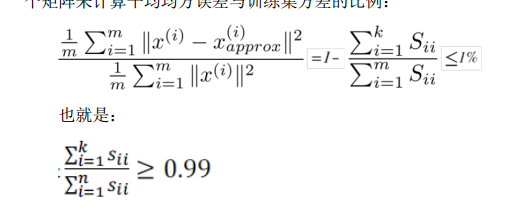
从而得到k的值。并且在压缩后,我们可以依据
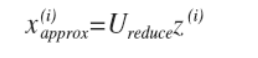
(其中 x approx ≈ x)来还原之前未被压缩的数据。
主成分分析法在机器学习过程中的应用:
例如,将100*100的图像压缩到1000个特征。
step 1)用PCA对特征值进行压缩
step 2)对训练集使用学习算法。
step 3)在预测时,采用学习得到的Ureduce将x特征转化成Z特征再进行预测。
使用时候可能存在的误区:
1)不要用PCA进行对过拟合的修正,此时可以尝试归一化。主要成分分析算法只是丢掉一些特征,不会考虑任何与结果有关的变量,这样做容易使对于本学习算法得重要的特征信息丢失。
2)降维不是所有机器学习算法的必要过程,因此不是所有的算法都要去使用,只是当算法运算太慢或者太消耗内存的时候,我们才会去考虑使用PCA算法进行优化。