测试误差
我们在拿到样本后进行机器学习，通常可以将样本分为两部分，比如前70%用来机器学习得到Θ，后30%用来对数据进行检验。
如何进行检验？
之前我们知道，逻辑回归代价函数JΘ的计算法方法，那么此处同理，我们可以得到对测试数据的JtestΘ的表达式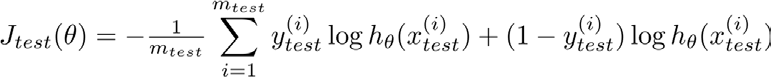
，然后，我们利用剩下的测试数据统计0 / 1错分率，（或称误分类率）error(hΘ(x),y)
,得到test error = ∑error(hΘ(x),y)/m_test【 i from 1 to m】。
对假设函数模型的选择
d的不同会有从低阶到高阶有（前面的标号为d的值，比如第一个式子中d的值就是1）
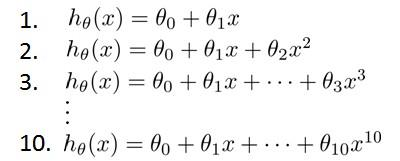
d = 1时候对应计算的Θ值记为Θ（1），计算的得到的代价函数记为Jtest(Θ(1))以此类推。随着d的增加，多项式的高次项越来越多，那么对于这么多的高次多项式，该如何选择？通常做法为
1）选取对误差分类率最小的hΘ（x）作为假设函数。
2）进行交叉验证：得到Jcv（Θ）
3）计算样本误差 Jtest（Θ）
上式中有J training error表示为测试误差J Cross Validation error表示为验证误差，J test error 表示为样本误差。
我们可以研究随着多项式的项数（次数） d 的增加，J training（Θ）和Jcv （Θ）的值，即error的变化情况。
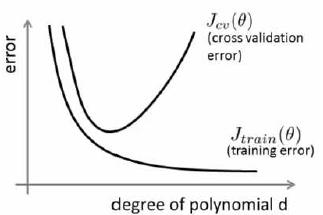
通过图像，我们可以得到一下结论
1）对于低次项（d较小）时候，容易出现高偏差，欠拟合的情况，此时Jtrain（Θ）的值较高，且Jcv（Θ）≈Jtrain（Θ）。
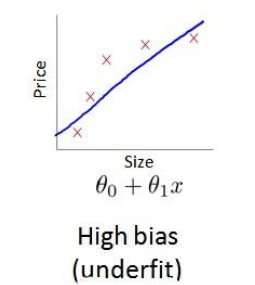
2）对于高次项（d较大）的时候，容易出现高方差，过拟合的情况，Jtrain（Θ）的值低，且Jcv（Θ）>>Jtrain（Θ）。
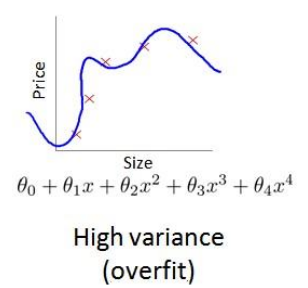
假设我们对hΘ（x）= Θ0+Θ1·x+Θ2·x^2+...+Θ4·x^4这样一个四次多项式进行拟合，为了防止过拟合，根据之前我们所学到的，可以对它进行正规化，添加一个正规化项以后，JΘ变为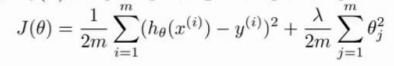
这时候，就需要选取一二适合的λ值，我们从λ = 0 到λ到10000逐渐测试，观察拟合图像。当λ等于0的时候，图像没有对参数惩罚，对应的是高方差的情况
当λ = 10000的适合，图像对参数惩罚十分严重，使其几乎为0，得到的图像是高偏差的情形。
：
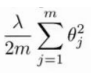（1）λ = 10000 →Θ1≈Θ2...≈Θ4≈0→hΘ（x）≈Θ0→高偏差，欠拟合的情况。
（2）λ参数合适 恰好拟合。
（3）λ = 0→Jcv>>Jtrain 高方差，过拟合
小结
因此选取λ的方法为：
1. 使用训练集训练出 12 个不同程度归一化的模型（得出minΘ对J（Θ））
2. 用 12 模型分别对交叉验证集计算的出交叉验证误差（得出对应的Θ（i））
3. 选择得出交叉验证误差最小的模型（得出Jcv（Θ））
4. 运用步骤 3 中选出模型对测试集计算得出推广误差（JtestΘ）,我们也可以同时将训练集和交叉验证集模型的代价函数误差与 λ 的值绘制在一张图表上：
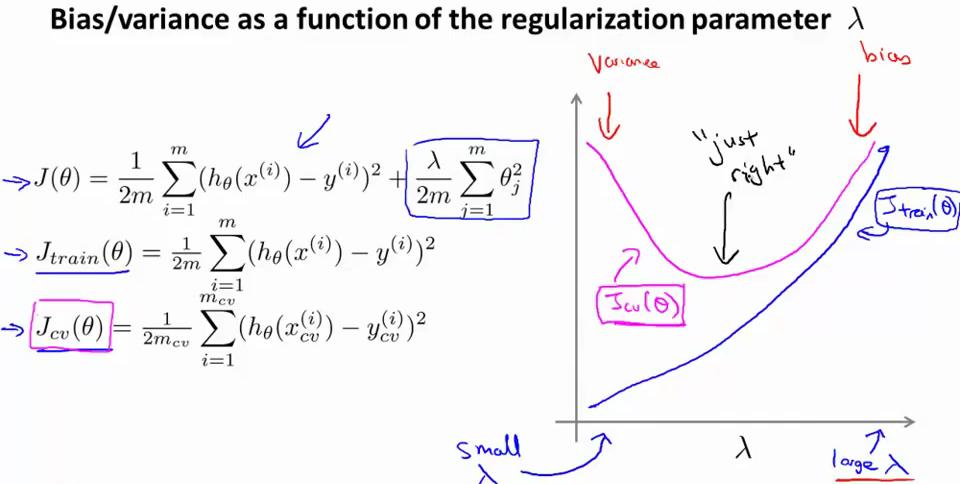
从图上，不难看出
• 当 λ 较小时,训练集误差较小(过拟合)而交叉验证集误差较大
• 随着 λ 的增加,训练集误差不断增加(欠拟合),而交叉验证集误差则是先减小后增加
训练样本m与error之间的关系 Learning curves
一简单的栗子，当训练样本数m从1到6时候，假设函数h的变化如图所示：
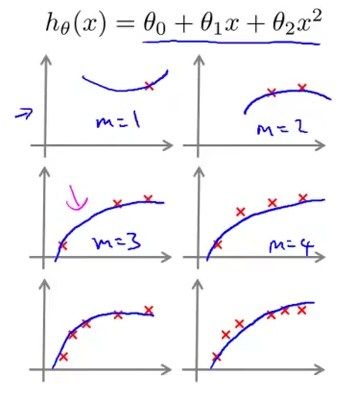
在前三个图的时候Jcv（Θ）还都几乎是零，不存在误差，可随着测试样本数m的逐渐增大，Jcv的值也随着m的增大而增大，导致了拟合效果的下降。
通过之前的观察，我们得出m与error之间的关系图像：
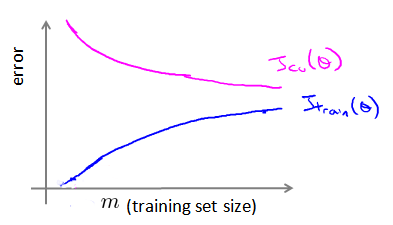
对高偏差的情况（High bias）：如果学习算法本身就有很大偏差，增加样本容量时候，对算法的误差改善没有帮助。
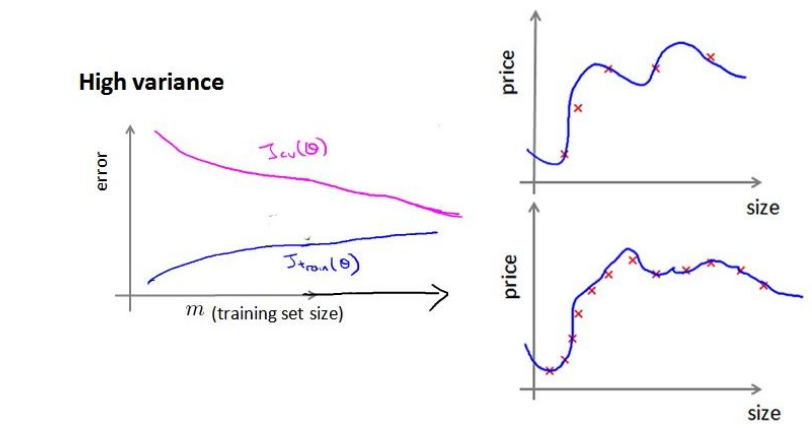
对高方差的情况（High variance）：在少样本容量时，Jcv（Θ）的值很大，Jtrain(Θ)的值很小，两者直接距离较远，只有在大量的样本容量时，增加样本容量，对改善算法误差值是有效果的。
总结：如何改善学习方法？How to debugging a learning algorithm
1：取得更多的训练样本（此方法对高方差情况有效果）
2：选取少的特征值（对高方差情况有效果）
3：增加特征值（对高偏差情况有效）
4：增加多的特征式，如x1^2，x2^2，x1x2,...（对高偏差情况有效）
5：减小λ的值（减小惩罚力度）。（对高偏差的情况有效）
6：增加λ的值（加大惩罚力度）。（对高方差的情况有效）
神经网络与过度拟合问题：
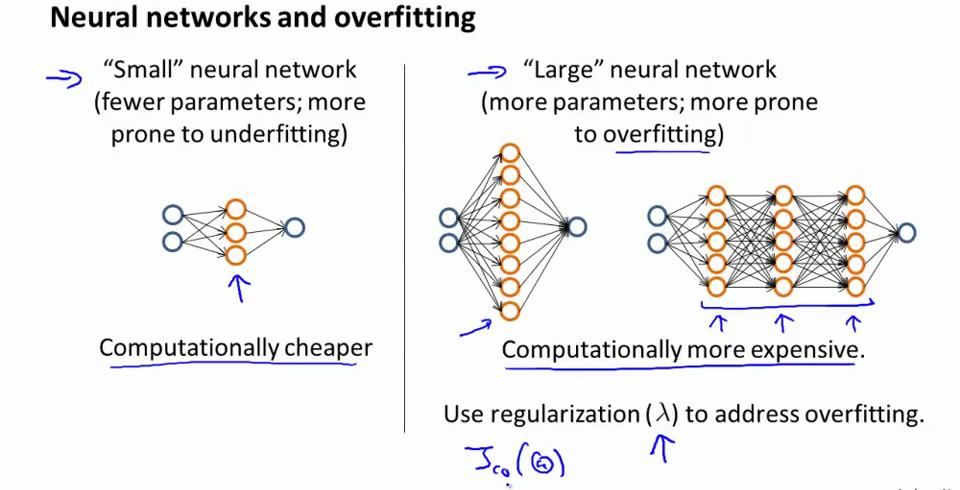
1：当对一个叫小的神经网络进行拟合的时候，可以选一个较小的，简单的神经网路结构，此时参数较少，容易出现欠拟合情况，但计算成本较低。
2：对一个相对较为复杂的神经网络，因为其中含有较多的隐藏层，容易出现较多的参数，过拟合情况容易发生。计算量较大。想要选择一个合适的隐藏层数，可以尝试对数据进行分割，分成训练集，验证集，测试集，然后改变隐藏层的数量进行测试，选取最佳的Jcv时候的隐藏层数。