Today Pari and Arya are playing a game called Remainders.
Pari chooses two positive integer x and k, and tells Arya k but not x. Arya have to find the value 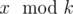 . There are n ancient numbers c1, c2, ..., cn and Pari has to tell Arya
. There are n ancient numbers c1, c2, ..., cn and Pari has to tell Arya 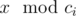 if Arya wants. Given k and the ancient values, tell us if Arya has a winning strategy independent of value of x or not. Formally, is it true that Arya can understand the value
if Arya wants. Given k and the ancient values, tell us if Arya has a winning strategy independent of value of x or not. Formally, is it true that Arya can understand the value 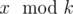 for any positive integer x?
for any positive integer x?
Note, that 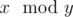 means the remainder of x after dividing it by y.
means the remainder of x after dividing it by y.
The first line of the input contains two integers n and k (1 ≤ n, k ≤ 1 000 000) — the number of ancient integers and value k that is chosen by Pari.
The second line contains n integers c1, c2, ..., cn (1 ≤ ci ≤ 1 000 000).
Print "Yes" (without quotes) if Arya has a winning strategy independent of value of x, or "No" (without quotes) otherwise.
4 5 2 3 5 12
Yes
2 7 2 3
No
In the first sample, Arya can understand 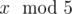 because 5 is one of the ancient numbers.
because 5 is one of the ancient numbers.
In the second sample, Arya can't be sure what 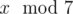 is. For example 1 and 7 have the same remainders after dividing by 2 and 3, but they differ in remainders after dividing by 7.
is. For example 1 and 7 have the same remainders after dividing by 2 and 3, but they differ in remainders after dividing by 7.
题意:给定k和n,给出n个ci,表示你可以知道x%ci。问能否唯一确定x
思路:首先,根据剩余定理,如果我们想知道x%m等于多少,当且仅当我们知道x%m1,x%m2..x%mr分别等于多少,其中m1m2...mr=m,并且mi相互互质,即构成独立剩余系。令m的素数分解为m=p1^k1p2^k2...pr^kr,如果任意i,都有pi^ki的倍数出现在集合中,那么m就能被猜出来。即k是否存在于素数集合或者存在k的整数倍。
#include <bits/stdc++.h>
using namespace std;
long long gcd(long long a,long long b){
if(b == 0) return a;
return gcd(b,a%b);
}
long long lcm(long long a,long long b){
return a*b/gcd(a,b);
}
int main()
{
int n,k;
while(cin>>n>>k){
int ans = 1;
int temp;
for(int i = 1;i <= n;i ++){
scanf("%d",&temp);
ans = gcd(k,lcm(ans,temp));
}
if(ans == k) cout<<"Yes"<<endl;
else
cout<<"No"<<endl;
}
return 0;
}