分治算法的核心思想是将一个规模很大的问题化简为n个规模较小的问题,这些子问题虽然独立而不同,但是问题的本质是一致的,从而达到分而治之的目的
- 归并排序
- 连续子列表的最大和
- 几何问题-凸包
- 数学问题-多项式乘法
归并排序
归并排序是一种有效的排序算法。其他常见的八种排序算法包括冒泡排序,插入排序,二叉树排序,快速排序,堆排序,希尔排序等
问题描述
将乱序的数列用归并算法将其排序输出
思路描述
归并算法有两种类型:递归法(Top-down) 和迭代法(Bottom-up)
递归法描述
递归法的核心思想是
-
把列表分为两个子列表,单独排序子列表再合并子列表。
-
如图,递归法可以利用二叉树理解:列表为根节点,子列表为子节点。

-
首先排序子列表,再一步步合并子列表
这个算法之所以称为递归法是因为它利用递归的思想,把根节点的问题递给子节点,一环套一环解决问题
迭代法描述
迭代法的核心思想是
-
利用for循环将列表的子列表成对排序合并,最后组成一个整体
-
如图,迭代法可以利用倒二叉树:对独立子列表(子节点) 进行多次迭代,直到完整列表(根节点)
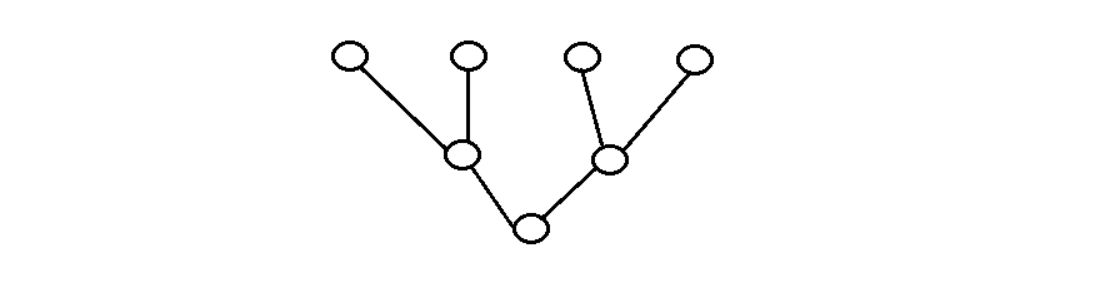
-
首先把列表看成n个长度为1的子列表,利用循环把相邻的两个子列表合并
-
得到 n/2 个长度为2的子列表
-
依次类推,最后得到长度为n的完整列表
代码实现
递归法
def merge_sort1(arr):
"""
递归法 归并排序
:param arr: 乱序数组
:return:
"""
if len(arr) < 2:
return
# 找到列表中点
cut = len(arr) // 2
# 左子列表
arr1 = arr[: cut]
# 右子列表
arr2 = arr[cut: ]
# 左子列表归并排序
merge_sort1(arr1)
# 右子列表归并排序
merge_sort1(arr2)
pointer1 = 0
pointer2 = 0
counter = 0
while pointer1 < len(arr1) and pointer2 < len(arr2):
if arr1[pointer1] < arr2[pointer2]:
arr[counter] = arr1[pointer1]
pointer1 += 1
else:
arr[counter] = arr2[pointer2]
pointer2 += 1
counter += 1
while pointer1 < len(arr1):
arr[counter] = arr1[pointer1]
pointer1 += 1
counter += 1
while pointer2 < len(arr2):
arr[counter] = arr2[pointer2]
pointer2 += 1
counter += 1
array = [2, 3, 4, 1, -2, 0, 5, 1]
merge_sort1(array)
print(array)
# >>>
迭代法
def merge_sort2(arr):
length = len(arr)
n = 1
while n < length:
for i in range(0, length, n*2):
arr1 = arr[i: i + n]
arr2 = arr[i + n: i + n*2]
pointer1 = 0
pointer2 = 0
counter = i
while pointer1 < len(arr1) and pointer2 < len(arr2):
if arr1[pointer1] < arr2[pointer2]:
arr[counter] = arr1[pointer1]
pointer1 += 1
else:
arr[counter] = arr2[pointer2]
pointer2 += 1
counter += 1
while pointer1 < len(arr1):
arr[counter] = arr1[pointer1]
pointer1 += 1
counter += 1
while pointer2 < len(arr2):
arr[counter] = arr2[pointer2]
pointer2 += 1
counter += 1
n = n*2
array = [2, 3, 4, 1, -2, 0, 5, 1]
merge_sort2(array)
print(array)
# >>>
连续子列表的最大和
问题描述
在一个列表中找出连续子列表的最大和,列表中的数字可负可正,并且子列表不能为空
思路解析
- 列表的最大子列表的和,有三种可能:左子列表,右子列表或左子列表与右子列表之间
- 左子列表和右子列表答案是知道的,找到左右子列表之间的子列表最大和就可以了
- 设一个中点,遍历中点左边的值,跟踪记录已遍历过的值的总和,取这些总和的最大值
- 遍历中点右边的值,同样跟踪记录已遍历过的值的总和,取这些总和的最大值
- 最后,左面的最大值+右面的最大值+中点值就是第三种可能的答案了
代码实现
def max_sub_array(arr):
if arr == []:
return
if len(arr) == 1:
return arr[0]
# 设中点
cut = len(arr) // 2
# 分治:找到左子列表最大和
left_sum = max_sub_array(arr[: cut])
# 分治:找到右子列表最大和
right_sum = max_sub_array(arr[cut: ])
left_middle_sum = 0
max_l = 0
right_middle_sum = 0
max_r = 0
# 找到左子列表与右子列表之间子列表的最大和
for i in range(cut - 1, -1, -1):
left_middle_sum += arr[i]
max_l = max(left_middle_sum, max_l)
for i in range(cut + 1, len(arr), 1):
right_middle_sum += arr[i]
max_r = max(right_middle_sum, max_r)
# 返回三种可能的最大值
return (max(left_sum, max_l + arr[cut] + max_r, right_sum))
arr = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
max_sum = max_sub_array(arr)
print(max_sum)
#>>>
几何问题--凸包
简单地讲,凸包是正好包含所有点的凸多边形。之所以叫凸包正是因为这个凸多边形包围所有点。
如图所示,所有红点包围住所有点
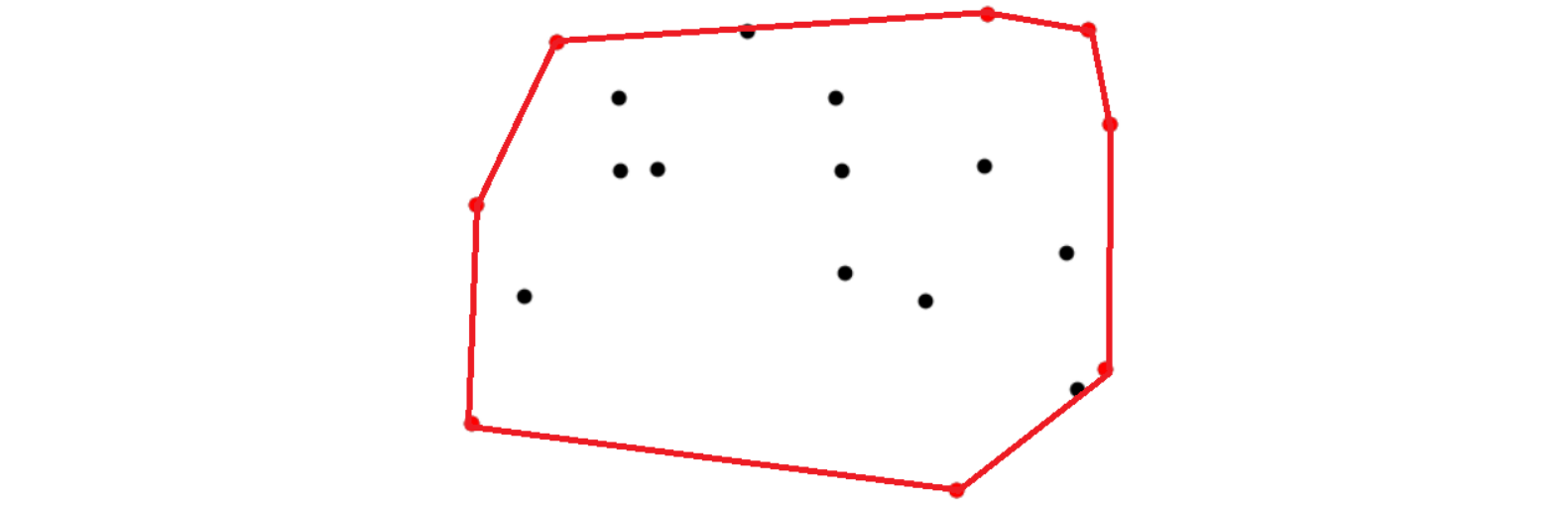
这个问题有不同的计算方式,常见的有分治法、Graham扫描法、Jarvis步进法、快包法
问题描述
在点集合中找出凸包的顶点集
思路解析
解决点与直线的位置判断
通过行列式的正负值判断直线与点之间的位置关系,同时数值为点与线段所围成的三角型面积
[egin{vmatrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1end{vmatrix}=x_1y_2 + x_2y_3 + x_3y_1 - x_3y_2 - x_2y_1 - x_1y_3
]
成立的前提条件是组成直线的两个点(x1,y1)和(x2,y2)必须满足x1 < x2,
点(x3,y3)必须是判断与直线关系的点
分治法思路解析
- 首先,找出横坐标最大、最小的两个点(P1, P2)所组成的直线L12,
- 用L12将点集合分成上下两个集合set1、set2
- 接下来,分别从set1、set2中中找出与直线L12构成面积最大的上下两个三角形的点(P3, P4)
- 从set1找出由点(P1, P3)组成的直线L13左侧的点集合left_set1
- 从set1找出由点(P2, P3)组成的直线L23右侧的点集合right_set1
- 将left_set1、right_set1 重复345步骤,直到找不到直线更外侧的点
- 同理从set2中找出left_set2,right_set2,重复步骤,直到找不到直线更外侧的点
代码实现
import numpy as np
import matplotlib.pyplot as plt
def cal_tri_area(p1, p2, p3):
"""
通过计算三角形(点P1,P2,P3)的面积(点在直线左边结果为正,直线右边结果为负)
来判断 P3相对于直线L1(点P1,P2)的位置
:param p1:
:param p2:
:param p3:
:return:
"""
size = p1[0] * p2[1] + p2[0] * p3[1] + p3[0] * p1[1] - p3[0] * p2[1] - p2[0] * p1[1] - p1[0] * p3[1]
return size
def far_point(seq, dot1, dot2, dot_set):
"""
找出据直线最远的点(该点与直线围成的三角形的面积为正且最大)
:param seq:
:param dot1:
:param dot2:
:param dot_set:
:return:
"""
# 负无穷大
max_size = np.NINF
max_dot = ()
online = []
max_set = []
for u in seq:
size = cal_tri_area(dot1, dot2, u)
# 判断点u是否能是三角形u dot1 dot2 的面积为正
if size < 0:
continue
elif size == 0:
online.append(u)
# 若面积为正,则判断是否是距离直线最远的点
if size > max_size:
if len(max_dot) > 0:
max_set.append(max_dot)
max_dot = u
max_size = size
else:
max_set.append(u)
# 结果判断
if not max_set:
# 没找到分割点,同时可能有点落在直线dot1 dot2上
if not max_dot:
dot_set.extend(online)
return [], ()
# 有分割点
else:
dot_set.append(max_dot)
return [], max_dot
# maxSet不为空
else:
dot_set.append(max_dot)
return max_set, max_dot
def near_point(seq, dot1, dot2, dot_set):
"""
找出据直线最远的点(该点与直线围成的三角形的面积为负数且最大)
:param seq:
:param dot1:
:param dot2:
:param dot_set:
:return:
"""
# 正无穷大
min_size = np.inf
min_dot = ()
online = []
min_set = []
for u in seq:
size = cal_tri_area(dot1, dot2, u)
# 判断点u是否能是三角形u dot1 dot2 的面积为负
if size > 0:
continue
elif size == 0:
online.append(u)
# 若面积为负,则判断是否是距离直线最远的点
if size < min_size:
if len(min_dot) > 0:
min_set.append(min_dot)
min_size = size
min_dot = u
else:
min_set.append(u)
# 结果判断
if not min_set:
# 没找到分割点,同时可能有点落在直线dot1 dot2上
if not min_dot:
dot_set.extend(online)
return [], ()
# 有分割点
else:
dot_set.append(min_dot)
return [], min_set
# maxSet不为空
else:
dot_set.append(min_dot)
return min_set, min_dot
def divide_up(seq, dot1, dot2, dot3, dot4, dot_set=None):
"""
上包的递归划分
:param seq:
:param dot1:
:param dot2:
:param dot3:
:param dot4:
:param dot_set:
:return:
"""
# 初始化第一次运行时的参数
if len(seq) == 0:
return dot_set
if dot_set is None:
dot_set = []
if len(seq) == 1:
dot_set.append(seq[0])
return dot_set
# 划分上包左边的点集
left_set, max_dot = far_point(seq, dot1, dot2, dot_set)
# 绘图检测
plt.title('up_left')
plt.axis([-110, 110, -110, 110])
plt.scatter([d[0] for d in seq], [d[1] for d in seq], color='blue')
plt.scatter([dot1[0], dot2[0]], [dot1[1], dot2[1]], color='orange')
# 最外侧的点
if max_dot:
plt.scatter(max_dot[0], max_dot[1], color='red')
plt.show()
# 对上包左包的点集进一步划分
if left_set:
divide_up(left_set, dot1, max_dot, max_dot, dot2, dot_set)
# 划分上包右边的点集
right_set, max_dot = far_point(seq, dot3, dot4, dot_set)
# 绘图检测
plt.title('up_right')
plt.axis([-110, 110, -110, 110])
plt.scatter([d[0] for d in seq], [d[1] for d in seq], color='blue')
plt.scatter([dot3[0], dot4[0]], [dot3[1], dot4[1]], color='orange')
#
if max_dot:
plt.scatter(max_dot[0], max_dot[1], color='red')
plt.show()
# 对上包右包的点集进一步划分
if right_set:
divide_up(right_set, dot3, max_dot, max_dot, dot4, dot_set)
return dot_set
def divide_down(seq, dot1, dot2, dot3, dot4, dot_set=None):
"""
下包的递归划分
:param seq:
:param dot1:
:param dot2:
:param dot3:
:param dot4:
:param dot_set:
:return:
"""
# 初始化第一次运行时的参数
if len(seq) == 0:
return dot_set
if dot_set is None:
dot_set = []
if len(seq) == 1:
dot_set.append(seq[0])
return dot_set
# 划分下包左边的点集
left_set, min_dot = near_point(seq, dot1, dot2, dot_set)
# 绘图检测
plt.title('down_left')
plt.axis([-110, 110, -110, 110])
plt.scatter([d[0] for d in seq], [d[1] for d in seq], color='blue')
plt.scatter([dot1[0], dot2[0]], [dot1[1], dot2[1]], color='orange')
#
if min_dot:
plt.scatter(min_dot[0], min_dot[1], color='red')
plt.show()
# 对下包的左包进行进一步划分
if left_set:
divide_down(left_set, dot1, min_dot, min_dot, dot2, dot_set)
# 划分下包右包的点集
right_set, min_dot = near_point(seq, dot3, dot4, dot_set)
# 绘图检测
plt.title('down_right')
plt.axis([-110, 110, -110, 110])
plt.scatter([d[0] for d in seq], [d[1] for d in seq], color='blue')
plt.scatter([dot3[0], dot4[0]], [dot3[1], dot4[1]], color='orange')
#
if min_dot:
plt.scatter(min_dot[0], min_dot[1], color='red')
plt.show()
# 对下包的右包进一步划分
if right_set:
divide_down(right_set, dot3, min_dot, min_dot, dot4, dot_set)
return dot_set
def divide_main(seq):
# 将序列中的点按横坐标升序排序
seq.sort()
res = []
# 获取横坐标做大、最小的点及横坐标中位数
dot1, dot2 = seq[0], seq[-1]
seq1, seq2 = [], []
max_size, min_size = np.NINF, np.inf
max_dot, min_dot = (), ()
# med_x = (seq[len(seq)//2][0] + seq[-len(seq)//2-1][0]) / 2
# 对序列划分为直线dot1 dot2左右两侧的点集并找出两个点集的距直线最远点
for u in seq[1:-1]:
size = cal_tri_area(dot1, dot2, u)
if size > 0:
if size > max_size:
if len(max_dot) > 0:
seq1.append(max_dot)
max_size = size
max_dot = u
continue
else:
seq1.append(u)
elif size < 0:
if size < min_size:
if len(min_dot) > 0:
seq2.append(min_dot)
min_size = size
min_dot = u
continue
else:
seq2.append(u)
# print('seq1', seq1, max_dot)
# print('seq2', seq2, min_dot)
# 调用内建递归函数
res1 = divide_up(seq1, dot1, max_dot, max_dot, dot2)
res2 = divide_down(seq2, dot1, min_dot, min_dot, dot2)
if res1 is not None:
res.extend(res1)
if res2 is not None:
res.extend(res2)
for u in [dot for dot in [dot1, dot2, max_dot, min_dot] if len(dot) > 0]:
res.append(u)
return res
seq = [i for i in zip(np.random.randint(-100, 100, 20), np.random.randint(-100, 100, 20))]
res = divide_main(seq)
plt.axis([-110, 110, -110, 110])
plt.title("Result")
plt.scatter([dot[0] for dot in seq], [dot[1] for dot in seq], color='black')
plt.scatter([dot[0] for dot in res], [dot[1] for dot in res], color='red')
plt.show()