前面算法在生活中不谈,算法的重要性不谈,直接说算法。
第2章 算法基础
2.1 插入排序
书中主要介绍了插入排序的思想,即对于数组A[0 ~ N - 1],长度为N。那么,升序的插入排序的过程即是从A[1]开始,先和A[0]比较,如果比A[0]小,那么将A[0]的元素顺序后移放置在A[1]中,将原本A[1]的元素插入在A[0]的位置上,同理再拿A[5]举例,如果比A[4]小,那么A[4]后移,继续比较A[3],如果还是小,A[3]后移,直到找到合适的位置进行插入,原书中提供的伪代码,我这里提供对应的C语言代码实现,方便各等级程序员阅读。

然后算法导论为我们提供了一个称之为循环不变式的概念,这个循环不变式能够有效的帮我们验证自己所写算法的正确性,说是循环不变式很神奇,本质就是我们算法开始和终止的那个条件,诸如上面的代码for循环仅仅是负责基本的Loop,而while循环的判定条件也就是反证这个循环不变式。循环不变式有三个特征(如插入算法为例,倘若一开始的数组就已经按照目的顺序,也就是不需要排序的话,那么应该无法进入反证循环不变式要求的条件),第一个特征即是初始化条件为真,i >= 0 and (留待插入的数字 大于 前一个数字) 这就是一个反证的循环不变式,这个式子的目的是保证符合条件的情况能进入正确的插入流程,所以现在说循环不变式在这里也就是每一次开始前要准备插入的数字前面的序列应该已经是有序的了,当插入完成后,下一个数字前的序列还是有序的,这也就是保持的意义,迭代之前为真,下一次迭代之前还为真,当终止时也就是整个循环到达了length长度外,那么为我们提供的性质也就是通过保持可以得到性质,A[N]这个元素之前的部分A[0 ~ N - 1],都应该是有序的。
之后算法导论为我们提供了一些伪代码的约定和案例,看过的,或者有一定C语言基础 || 其他语言基础的程序员们都比较好理解了。
习题敲了一个2.1-4
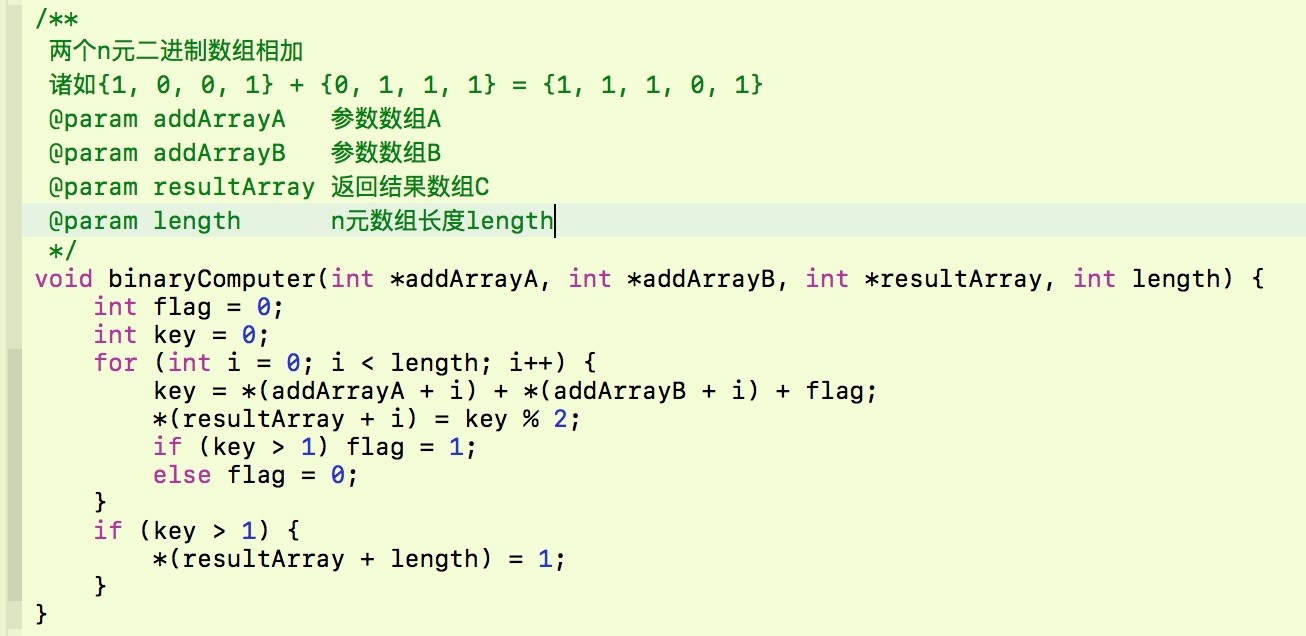
然后是算法的分析,其实就是为后面的时间复杂度做一定的铺垫,通过计算算法最优和最劣的情况,将算法可能执行的时间进行抽象。
习题中有选择排序,先贴代码把,准备睡觉
