计算几何

内容讲解的博客：计算几何初步

下面我们来逐步学习计算几何。

前置技能

先补充点英语：

slope 斜率

intersection 交点

half plain intersection 半平面交(hpi)

area 面积

再看一段代码：


struct vectors {
	double x;
	double y;
	vectors(double xx = 0, double yy = 0) {x = xx, y = yy; }
	vectors operator +(const vectors a)const {
		return vectors(x + a.x, y + a.y);
	}
	vectors operator -(const vectors a)const {
		return vectors(x - a.x, y - a.y);
	}
	double operator *(const vectors a)const {
		return x * a.y - y * a.x;
	}
};
inline double get_dis(vectors a, vectors b) {//两点间距离
	return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
inline double dot(vectors a, vectors b) {//点乘 
	return a.x * b.x + a.y * b.y;
}
inline double len(vectors a) {//模长 
	return sqrt(a.x * a.x + a.y * a.y);
}
inline vectors turn(vectors a, double n) {//旋转n
	return vectors(a.x * cos(n) - a.y * sin(n), a.x * sin(n) + a.y * cos(n));
}
inline double dis(const vectors a, const vectors b, const vectors x) {//x点到线段ab的距离
	return fabs(1.0 * ((a - x) * (b - x)) / get_dis(a, b));
}
inline vectors jiaodot(vectors A, vectors B, vectors C, vectors D) {//求交点
	//double t1 = AC * AB, t2 = AB * AD;
	double t1 = (C - A) * (B - A), t2 = (B - A) * (D - A);
	//double t3 = CA * CD, t4 = CD * CB
	return vectors((C.x * t2 + D.x * t1) / (t1 + t2), (C.y * t2 + D.y * t1) / (t1 + t2));
	/* 非严格相交：
		叉积为0，说明共线。
		1.4个叉积都为0： 4点共线
		2.2个叉积为0: 三个共线，一个共点
		3.1个叉积为0：三点共线 //先判断点是否在线段上，让后与情况2合并
	*/ 
}
inline vectors get_intersection(segments ab, segments cd){//直线相交，无需判断叉积为0的情况，但需保证无平行直线
	vectors A = ab.a, B = ab.b, C = cd.a, D = cd.b;
	double t1 = (C - A) * (B - A), t2 = (B - A) * (D - A);
		//AC -> AB -> AD，顺则同顺，逆则同逆 
   return vectors(C.x * t2 + D.x * t1) / (t1 + t2), (C.y * t2 + D.y * t1) / (t1 + t2));
   //= C + CD * t1 / (t1 + t2)
   //= (t1 * D + t2 * C) / (t1 + t2)
}

总而言之，我们可以用向量的缩放、旋转等操作来干好多事情。

三角剖分

利用叉积的几何意义（平行四边形的有向面积）以及容斥的思想来实现。

实现其实非常简单：

[S = frac{OA_1 × OA_2 + OA_2 × OA_3 + ... + OA_n × OA_1} {2} ]

位置判断

如何判断一个点在一条直线的左边还是右边还是直线上？

直接叉积。

在一条直线上，如何判断点是在一个线段上还是线段两边？

直接点积。

如何判断两个点是否在一条直线的两端？

跨立实验。分别判断每个点对于直线的方向，分类讨论即可。

如何判断一个点在凸包内部还是外部？

~~尝试将其加入凸包，成功则为外部，否则为内部~~

如图

点与凸包

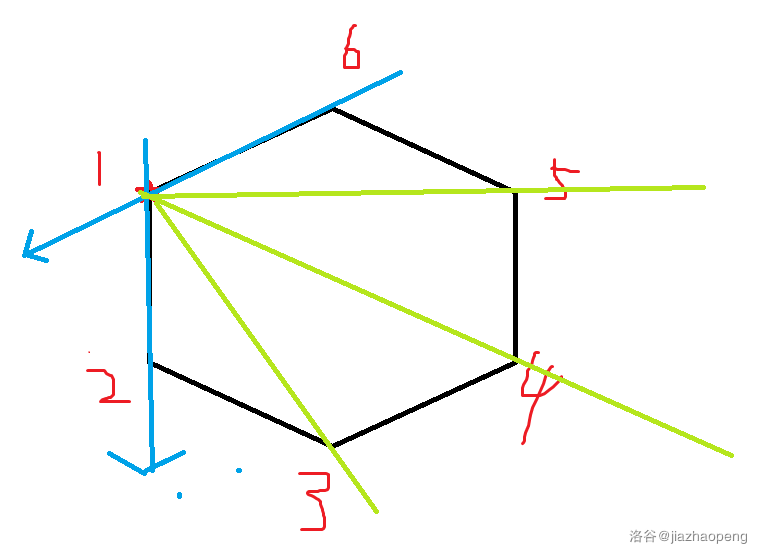
以1号点为基准，将平面分割成若干区域，蓝线右边的区域可以直接特判，内部的区域可以 lower_bound 快速查找点所在的区域，判断是否在凸包内部即可。

复杂度：(O(nlogn+qlogn))

//tmp[] 存一个凸包
vectors vec[N];
vectors bian1, bian2;//两边界
inline void build() {
	bian1 = tmp[2] - tmp[1], bian2 = tmp[1] - tmp[tot];//Attention!! - not =
	for (register int i = 2; i <= tot;++i) vec[i] = tmp[i] - tmp[1];
}

inline ll dot(vectors a, vectors b) {
	return 1ll * a.x * b.x + 1ll * a.y * b.y;
}

inline bool che(int x, int y) {
	vectors v(x, y);
	if ((v - tmp[1]) * bian1 > 0)	return false;
	if ((v - tmp[1]) * bian2 > 0)	return false;
	int p = lower_bound(vec + 2, vec + tot + 1, v - tmp[1]) - vec;//Attention!! : v - tmp[1]
	if ((v - tmp[1]) * (vec[p] - v) == 0) {
		if (dot(v - tmp[1], vec[p] - v) >= 0)	return true;
		else	return false;
	}
	if ((tmp[p] - v) * (v - tmp[p - 1]) == 0)	return true;
	if ((tmp[p] - tmp[p - 1]) * (v - tmp[p - 1]) > 0)	return true;
	return false;
}

如何判断一个点在多边形内部还是外部？

从这个点引一条射线,扫一遍所有边，判断是否和这条射线相交（或者从无穷远的地方选一个点作为射线另一端点，依次做跨立实验），如果相交数量为奇数，则在内部，否则在外部。

复杂度：(O(qn))

凸包

凸包性质：

周长最小，并且能包围所有给定点。
如果按逆时针方向看，凸包上每两条相邻的边都是向左拐的。也就是说，逆时针枚举边，相邻边应该逆时针转，叉积大于0。

凸包的求法

例题：P2742 【模板】二维凸包 / [USACO5.1]圈奶牛Fencing the Cows

利用凸包的性质2，我们将各点按横坐标排序，然后从左向右求下凸包，从右向左求上凸包。

具体来说，用单调栈维护凸包，用凸包的性质2来判断是否合法。

(Code:)

sort(v + 1, v + 1 + n, cmp);
sta[++top] = 1;//vis[1]先不等于0 
for (register int i = 2; i <= n; ++i) {//升序枚举下凸壳（凸壳逆时针） 
	while (top > 1 && (v[sta[top]] - v[sta[top - 1]]) * (v[i] - v[sta[top]]) <= 0) {
		vis[sta[top--]] = false;		//叉积<0,共线或顺时针旋转，不符合要求 
	}
	vis[i] = true;
	sta[++top] = i;
}
int tmp = top;//防止弹掉下凸壳的栈顶元素 
for (register int i = n - 1; i; --i) {//降序枚举上凸壳（凸壳逆时针）
	if (vis[i])	continue;
	while (top > tmp && (v[sta[top]] - v[sta[top - 1]]) * (v[i] - v[sta[top]]) <= 0) {
		vis[sta[top--]] = false;
	}
	vis[i] = true;
	sta[++top] = i;
}
//此时sta数组存储凸包上的点编号，sta[1] = sta[top] = 起始点 
memcpy(oldv, v, sizeof(v));
for (register int i = 1; i <= top; ++i)
	v[i] = oldv[sta[i]];

注意一下细节。时间复杂度：O(nlogn)（排序）

习题：

其实这三道题是一种题型。其中信用卡凸包难度较大，涉及到向量旋转。所以我认为先做城墙为宜

P2521 [HAOI2011]防线修建

动态凸包的维护（支持加点）。用set代替stack维护即可。

注意：

首先先不让vis[1]=true；最后的sta数组sta[1] = sta[n]。

记得双关键字排序！！！！！第二关键字怎么排序都行，但就是要求有序！！！

旋转卡壳

旋转卡壳可以求凸包直径等问题。

例题：P1452 Beauty Contest /【模板】旋转卡壳

具体操作是：枚举每条边，找出边的对踵点，计算对踵点到边两端点距离，直径的长就一定会在这些距离中了。

如果我们逆时针枚举边，那么对踵点一定会逆时针地出现，符合单调的性质。又因为逆时针枚举对踵点，点到边的距离是单峰函数，所以我们找对踵点可以单方向枚举，搞一个类似于单调栈的东西。最后直径就取一个 (max) 即可。

注意：

不要让枚举的对踵点超出范围，要搞一个循环。
当“凸包”只有两个点时，这个算法会陷入死循环。所以要实现判一下有没有凸包。
求出凸包后，v[1] = v[top] = 最左下点

(Code:)

inline double get_h(vectors A, vectors b, vectors c) {
	return F((b - A) * (c - A)) / get_len(b - c);
}

...

if (top - 1 <= 2) {
	ans = get_len(v[1] - v[2]);
	...
	return 0;
}
int id = 1;
for (register int i = 1; i < top; ++i) {
	while (get_h(v[id], v[i], v[i + 1]) <= get_h(v[id + 1], v[i], v[i + 1])) {
		id++;
		if (id == top)	id = 1;
	}
	ans = max(ans, max(get_len(v[id] - v[i]), get_len(v[id] - v[i + 1])));
}

旋转卡壳还可以做很多事情，比如

求覆盖凸包的最小矩形面积：

UVA10173 Smallest Bounding Rectangle

P3187 [HNOI2007]最小矩形覆盖

求所有点中能组成的最大四边形面积

P4166 [SCOI2007]最大土地面积

（大多是猜想答案在对踵点上，然后用旋转卡壳来做）

半平面交

求同在多个直线的左边的点集。

极角排序

因为这里涉及到了对一堆平面内的线段排序，我们适用极角排序。需要使用atan2(double y, double x)函数。（注意先是y后是x）；

当极角一样是，我们按照从左到右的顺序排序（因为只有最左边的直线有用，使用时判一下 if (s[i].slop != s[i - 1].slop) 即可）。

维护双端队列

根据极角将直线逐个加入到单调队列里面。加入前判断队尾交点是否在当前直线的右边，如果交点都在右边，说明队尾直线就没用了，直接删掉就好。考虑到可能当前直线可能会约束队首，因此也要判断一下队首的直线交点是否在右边，在则删除。

最后，可能队尾会有一些不合法的直线，用队首排除队尾，再用队尾排除队首即可。

(Code:)

inline vectors inter(segments ab, segments cd) {
	vectors A = ab.a, B = ab.b, C = cd.a, D = cd.b;	
	double t1 = (C - A) * (B - A), t2 = (B - A) * (D - A);//AC -> AB -> AD	
	//attention!!!
	return vectors((C.x * t2 + D.x * t1) / (t1 + t2), (C.y * t2 + D.y * t1) / (t1 + t2));
}

bool cmp(const segments &a, const segments &b) {
	if (a.slop != b.slop)	return a.slop < b.slop;
	return (a.b - a.a) * (b.b - a.a) < 0;
}

inline bool che(segments ab, segments cd, segments l) {
	vectors inters = inter(ab, cd);
	return (l.b - l.a) * (inters - l.a) <= 0;
}

int main() {

	...(get in)
    
	for (register int i = 1; i <= tot; ++i) {
		vectors vec = s[i].b - s[i].a;
		s[i].slop = atan2(vec.y, vec.x);
	}
	sort(s + 1, s + 1 + tot, cmp);
    
	que[++rear] = s[1];
	for (register int i = 2; i <= tot; ++i) {
		if (F(s[i].slop - s[i - 1].slop) < eps)	continue;
		while (front < rear - 1 && che(que[rear - 1], que[rear], s[i]))	rear--;
		while (front + 1 < rear && che(que[front + 1], que[front + 2], s[i]))	front++;
		que[++rear] = s[i];
	}
    
	while (front < rear - 1 && che(que[rear], que[rear - 1], que[front + 1]))	rear--;
	while (front + 1 < rear && che(que[front + 1], que[front + 2], que[rear]))	front++;
   
	int top = 0;
	que[rear + 1] = que[front + 1];
	for (register int i = front + 1; i <= rear; ++i) {
		inters[++top] = inter(que[i], que[i + 1]);
	}

注意！！

要先排除队尾，后排除队首，不然据说会出错。
判断交点记得是t1 = AC * AB, t2 = AB * AD;，就这样写，不然会奇怪地出错。我也不知道为啥，可能这种写法对处理直线不仅只在第一象限，或者直线所用线段不交等情况更有优势吧。
此时(cnt,tot,top,front, rear)等变量名较多，注意区分。

练习题

P2600 [ZJOI2008]瞭望塔

猜想发现答案一定存在一些特殊点：拐点上，因此求出半平面交，然后 (n^2) 枚举特殊点都行。

注意 添加左右边界 以算出边界交点。（当然，这也是半平面交中的常见做法)

最小圆覆盖（随机增量法）

P1742 最小圆覆盖

给定一个点集，要用最小的圆覆盖所有点。

显然，点集中一定有至少两个点再这个最小的圆上。并且，如果我们知道其中的三个点，就能知道这个圆。于是我们已经会写 (O(n^3)) 的暴力了。

正解依赖随机化算法。随机打乱点。先枚举一个不在当前圆上的点 (P_i)，并且把当前圆设定为圆心为 (P_i)，半径为 0 的圆。再从 (1) 到 (i) 枚举一个不在圆上的点 (P_j)，并且把当前圆设定为直径为两点连线的圆。然后再从 (1) 到 (j) 枚举一个不在圆上的点 (P_k)，并且把当前圆设定为过 (P_i, P_j, P_k) 的圆。循环结束不清空圆，最终答案即为所求圆。

复杂度：期望 (O(n))

关键代码：

//fan() : 翻转90度:(x, y) -> (y, -x)
inline vectors get_inter(vectors a, vectors b, vectors c, vectors d) {//求中垂线交点
	vectors mid = get_mid(a, b);
	b = mid + (b - a).fan();
	a = mid;
	mid = get_mid(c, d);
	d = mid + (d - c).fan();
	c = mid;
	double t1 = (c - a) * (b - a), t2 = (b - a) * (d - a);
	return vectors((c.x * t2 + d.x * t1) / (t1 + t2), (c.y * t2 + d.y * t1) / (t1 + t2));
}
inline Circle get_cir(vectors a, vectors b, vectors c) {
	if (F((b - a) * (c - b)) <= eps)	return Circle(vectors(0, 0), 0);
	vectors vec = get_inter(a, b, b, c);
	return Circle(vec, (vec - a).get_len());
}
(int main())
...
	random_shuffle(h + 1, h + 1 + n);
    Circle cir(vectors(0, 0), 0.0);
    for (register int i =1 ; i <= n; ++i) {
		if (!cir.che(h[i])) {
			cir = Circle(h[i], 0);
			for (register int j = 1; j < i; ++j) {
				if (!cir.che(h[j])) {
					cir = Circle(get_mid(h[i], h[j]), 0.5 * (h[j] - h[i]).get_len());
					for (register int k = 1; k < j; ++k) {
						if (!cir.che(h[k])) {
							cir = get_cir(h[i], h[j], h[k]);
						}
					}
				}
			}
		}
	}
}

闵可夫斯基和

已知两凸包 (A, B)，求一个凸包 (C)，满足 (forall p in A, p' in B, (p+p') in C)。

我们同时从两个凸包的最左边（或左上角之类的）开始走（事先已经合成了 (C) 中对应的那个点)，每次选择两个凸包中最靠“右”的那一条边在 (C) 上走，最终走回原来的那个点，所形成的那个凸包即为 (C)。最后最好再把 (C) 扔回去再求一遍凸包，去掉一些重边。

闵可夫斯基和可以处理凸包与凸包是否有公共点问题：将凸包 (B) 关于原点对称，(A, B) 做一遍闵可夫斯基和，合成一个凸包 (C)，查询 ((0, 0)) 是否在 (C) 内即可。原理：公共点 ((x, y)) -> ((x, y) + (-x, -y) = 0)。

关键代码：

int t1, t2, tot;
vectors tmp[N];
inline void Merge() {
	tot = 0;
	t1 = t2 = 1;
	tmp[++tot] = h1[t1] + h2[t1];
	while (t1 <= n && t2 <= m) {
		if ((h1[t1 + 1] - h1[t1]) * (h2[t2 + 1] - h2[t2]) >= 0)
			++tot, tmp[tot] = tmp[tot - 1] + (h1[t1 + 1] - h1[t1]), ++t1;
		else	++tot, tmp[tot] = tmp[tot - 1] + (h2[t2 + 1] - h2[t2]), ++t2;
	}
	while (t1 <= n)
		++tot, tmp[tot] = tmp[tot - 1] + (h1[t1 + 1] - h1[t1]), ++t1;
	while (t2 <= m)
		++tot, tmp[tot] = tmp[tot - 1] + (h2[t2 + 1] - h2[t2]), ++t2;
	get_tubao(tmp, tot - 1);
	tot = top - 1, top = 0;
}

题

平面图转对偶图

众所周知，平面图最小割 = 对偶图最短路，因此平面图转对偶图可以优化网络流。

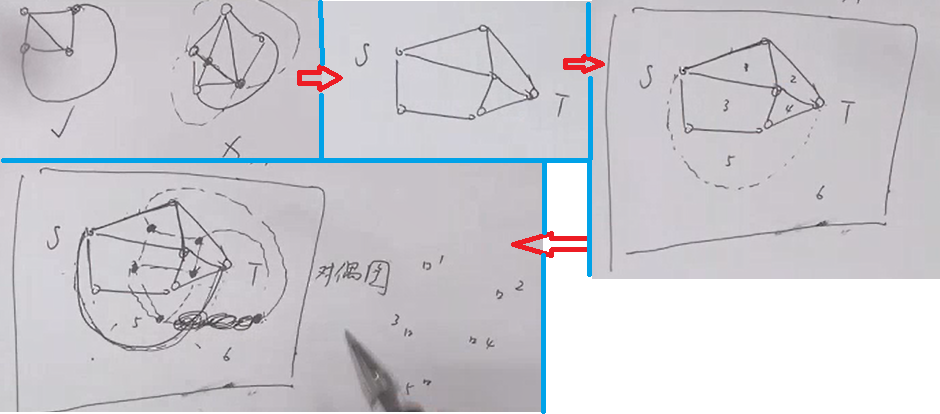
平面图对偶图

然而有时候平面图并不一定是网格图，对偶图也不一定只用在网络流。对偶图还可以把平面区域转化为点，把平面区域之间的边转化为边，方便做题。

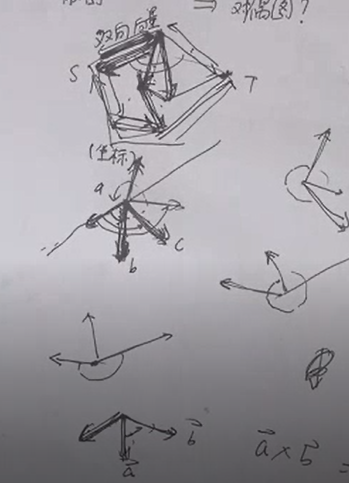
最小左转法

先去除平面图中多余的边，然后把平面图的边拆成双向边，随便选择一条没有经过的边，从它开始，从出点的出边里面选择这条边对应边的顺时针方向第一条边，将其作为下一条边，直到围成一个区域。然后继续这种操作直到所有边都被经过。

“下一条边”可以通过极角排序维护，区域的面积可以通过三角剖分求，注意有一个“无限大”区域，其面积为负数（整个平面图的面积的相反数）

计算几何对偶图

例题：

P3249 [HNOI2016]矿区

建对偶图 + 生成树上容斥

关键代码：

struct Edge{
	int v, id; double deg;
	Edge(int uu, int vv, int idd, double degg) { v = vv, id = idd, deg = degg; }
	Edge(int uu, int vv, int idd) {
		v = vv, id = idd;
		vectors vec = vt[vv] - vt[uu];
		deg = atan2(vec.y, vec.x);
	}
	bool operator <(const Edge a) const {
		return deg - a.deg < -eps;
	}
};
vector<Edge> E[N];
int opppos[NN], opid[NN], Nxtpos[NN];
//pos:下标；id：编号
inline void init() {//预处理“下一条边”
	for (register int i = 1; i <= n; ++i)
		sort(E[i].begin(), E[i].end());
	for (register int cur = 1; cur <= n; ++cur) {
		for (register uint i = 0; i < E[cur].size(); ++i) {
			int to = E[cur][i].v, nwe = E[cur][i].id;
			
			int tmp = lower_bound(E[to].begin(), E[to].end(), Edge(to, cur, opid[nwe])) - E[to].begin();
			opppos[nwe] = tmp;
			if (tmp == 0)	tmp = E[to].size() - 1;
			else	--tmp;
			Nxtpos[nwe] = tmp;
		}
	}
}
inline void build() {
//找出所有区域并标记原图“边”左右区域
	for (register int i = 1; i <= n; ++i) {
		for (register uint j = 0; j < E[i].size(); ++j) {
			int nwe = E[i][j].id;
			if (lft[nwe])	continue;
			++ctot;
			int np = i, nxtp = E[i][j].v;
			S[ctot] += vt[np] * vt[nxtp];
			lft[nwe] = ctot, rgt[opid[nwe]] = ctot;
			do {
				Edge tmp = E[nxtp][Nxtpos[nwe]];
				np = nxtp; nxtp = tmp.v;
				nwe = tmp.id;
				S[ctot] += vt[np] * vt[nxtp];
				lft[nwe] = ctot; rgt[opid[nwe]] = ctot;
			} while (nxtp != i);
			if (S[ctot] < 0)	Rt = ctot;
		}
	}
}

#2965. 保护古迹

点被围起来 = 点不与最外面联通

因此建立对偶图，暴力枚举点集，求最小割。

多源点最小割？超级源点！

#2960. 跨平面

建对偶图 + （无根）最小树形图。

平面图上点定位

在学了...

计算几何中需要注意的东西

计算几何中经常用到小数运算，这时注意精度问题（记得加 (eps)）。判相等的时候用绝对值差不超过 (eps) 来判断，但是判大小的时候不能这么用，应该直接判大小！！
在求凸包和旋转卡壳的while中，注意是<=而不是<。
注意叉乘乘出来的是有向面积！
(a, b, x, y) 之类的注意一下，不要打错字母了！

相关阅读:
转：用两个栈实现一个队列——我作为面试官的小结
 Android屏幕重力感应旋转
 简单的单例模板，继承使用即可
 cocos2dx windows 音量设置无效解决办法
 lua lu
OpenGL ES API with no current context
git更新某个目录
 sh ndk-build clean Cannot run program "sh": Launching failed Error: Program "sh" not found in PATH PATH=......
sublime Text快捷键
 转：解决windows下eclipse中android项目关联android library project失败问题
原文地址：https://www.cnblogs.com/JiaZP/p/13389156.html

计算几何

内容讲解的博客： 计算几何初步

前置技能

三角剖分

位置判断

凸包

例题：P2742 【模板】二维凸包 / [USACO5.1]圈奶牛Fencing the Cows

习题：

注意：

旋转卡壳

例题：P1452 Beauty Contest /【模板】旋转卡壳

半平面交

极角排序

维护双端队列

注意！！

练习题

最小圆覆盖（随机增量法）

闵可夫斯基和

平面图转对偶图

最小左转法

例题：

P3249 [HNOI2016]矿区

#2965. 保护古迹

#2960. 跨平面

平面图上点定位

计算几何中需要注意的东西

内容讲解的博客：计算几何初步