第一个能看懂的论文:国家集训队2017论文集
这是我第一个自己理解的自动机(AC自动机不懂KMP硬背,SAM看不懂一堆引理定理硬背)
参考文献:2017国家集训队论文集 回文树及其应用 翁文涛
参考博客:回文树
一些定义
-
(回文)子串不包括空串。
-
(回文)后缀不包括原串本身,如果找不到,就是空串。
-
定义 (len[cur]) 为 (cur) 节点的代表串长度,(son[p][c]) 表示一条转移路径,(fail) 表示失配指针。
-
定义 (Sigma) 为字符集大小。
-
(c) 通常表示字符,(s) 或者 (S) 通常代表字符串,(p,cur) 代表节点。
-
有时我可能会将“回文串”和“回文树上代表其的节点”混用。
回文树原理及构造
回文树的结构
回文树由两棵树组成,一棵奇树,一棵偶树。
每个节点代表恰好一个回文串,每个原串的回文子串恰好有一个对应节点。
奇树上的点长度都为奇数,偶树上的点长度都为偶数。特别地,奇树根节点(通常编号为1)的长度为 -1,偶树根节点(通常编号为0)的长度为 0.
每个点都有一个 (fail) 指针,指向当前串的最长回文后缀。众多 (fail) 构成一棵以 1 为根的 (fail) 树,其中父亲为儿子的最长回文后缀;满足 (len[fa] < len[son]);并且一个回文串的所有回文后缀为从该节点到根节点 1 所经过的链上 (len) 为正数的回文串。
节点数和转移(边)数
可以证明,一个字符串的本质不同的回文子串数量不超过字符串长度,因此回文树节点数为 (O(|s|))。证明如下:
考虑新加入一个字符 (c) 所新增的位置不同的回文子串:(s[l_1, n], s[l_2, n], ...),那么除了 (s[l_1, n]) 外,其它的回文子串在之前一定已经出现过了(如图)。因此加 (c) 新增的本质不同的回文子串一定是 (s[1, n]) 的最长回文后缀。
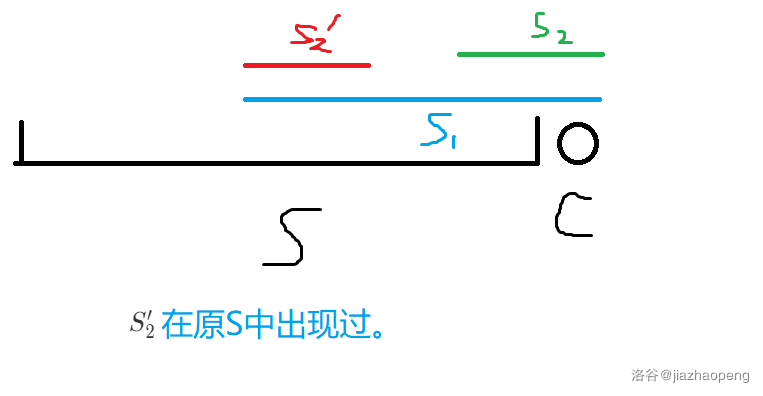
由于每个节点最多只由一个节点转移过来,因此回文树有 (O(|S|)) 边。(fail) 树上的边显然也是 (O(|S|))。
构造
增量法。
显然,每次我们只需搞出当前串的最长回文后缀即可。由于当前的最长回文后缀一定是先前的一个回文后缀加一个字符,我们可以直接在先前的最长回文后缀上暴跳 (fail) 链,直到合法位置((s[i - 1 - len[p]] == s[i]))。显然这是一定合法的,因为 (fail~tree) 的根节点长度为 -1,而 (s[i - 1 - (-1)] == s[i]) 一定成立。
然后再用类似的方法搞出当前点的 (fail) 指针(最长回文后缀).(len, son) 随便维护一下即可。
值得注意的是,每添加一个字符,最多只会改 (fail, len, son) 数组中的一个位置。
关键代码
int son[N][26], fail[N], lst, len[N], tot;
inline void init() {
len[1] = -1;
fail[1] = fail[0] = tot = 1;
}
inline int ins(int pos, int c) {
int p = lst;
while (s[pos - 1 - len[p]] != s[pos]) p = fail[p];
if (son[p][c]) return Len[lst = son[p][c]];
int np = ++tot, x = fail[p];
while (s[pos - 1 - len[x]] != s[pos]) x = fail[x];
fail[np] = son[x][c];
len[np] = len[p] + 2;
son[p][c] = np;
return Len[lst = np];
}
复杂度
分析一下时间复杂度。势能分析瞎搞搞就可以了。 我们死盯一个量:当前的节点在 (fail~tree) 上的深度。我们发现,每跳一次 (fail) 这个值会减一;每插入一个字符,这个值会加一。这个值始终非负,而最多加了 (|S|)。因此时间复杂度是 (O(|S|)) 的。
因此,时间 (O(|S|)),空间 (O(|S|Sigma))。
如果 (Sigma) 比较大,可以使用 (map) 存储 (son),时间 (O(|S|logSigma)),空间 (O(|S|))
拓展
支持前后加字符
与向后加字符类似,我们可以维护最长回文后缀的指针 (fail'),形成两棵 (fail~tree) 。并且我们发现一个神奇的性质:如果一个回文串 (t) 的最长回文后缀为 (t[i...|t|]),那么根据回文串的对称性,其最长回文前缀为 (t[1...|t|-i+1]),并且这两个回文串是一样的。也就是说, (fail) 指针和 (fail') 指针指向的是同一个节点 !那么我们就方便很多了,只需要多维护个 (lst),前后插入字符的同时都维护一下 (fail) 指针,整棵树的形态就是对的。
唯一一点需要注意的是,我们在前面插入一个字符 (c),最当前串的最长回文后缀可能产生影响,当且仅当插入 (c) 后整个串是一个回文串(显然)。因此注意修改后缀的 (lst)。后面插入对前缀的影响同理。