bzoj4246: 两个人的星座

题目描述：

 $JOI$ 酱和 $IOI$ 酱是好朋友。某天， $JOI$ 酱与 $IOI$ 酱决定去山上的某个展望台进行天体观测。

从展望台上可以观测到 $N$ 颗星星，编号为 $1...N$ 。每颗星星的颜色为红色、蓝色、黄色中的一种。

在展望台上观测到的星星可以用坐标系上的点来表示。在坐标系上，星 $i(1<=i<=N)$ 对应的点为 $Pi(Xi,Yi)$ 。坐标系上的点两两不同，且不存在三点共线。

 $JOI$ 酱和 $IOI$ 酱想要设立一个叫做“ $JOIOI$ 座”的星座。首先。两个人决定使用红色、蓝色、黄色三种颜色的星各一个构成的三角形。他们将这样的三角形称作“好三角形”。

两人将满足以下条件的好三角形无序二元组作为 $JOIOI$ 座的候补：

两个三角形没有公共点(包括内部和边界)。换言之，两个三角形之间既不相交，也不存在某个三角形包含另一个三角形。

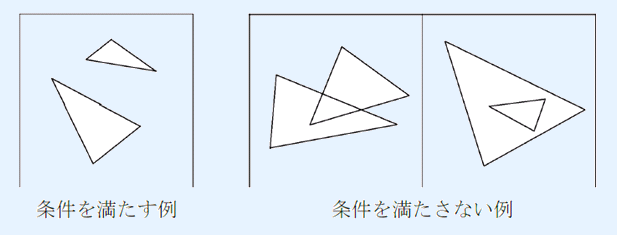
 $JOI$ 酱和 $IOI$ 酱想知道构成 $JOIOI$ 座的候补一共有多少种方案。

注意如果构成三角形的 $6$ 个点一样但是构成三角形的方式不同，算作不同的方案。

现在给出展望台上能观测到的星星的信息，请求出构成 $JOIOI$ 座的候补一共有多少种方案

思路：

对于两个不相交的三角形，连接两个三角形的顶点，必然有且仅有两条使得两个三角形在这条直线的两侧，考虑枚举这条直线，固定一个点后，按与这个点构成直线的斜率排序，每次转换角度维护在这条直线两侧的点每种颜色的个数。

以下代码：

#include<bits/stdc++.h>
#define il inline
#define db double
#define LL long long
#define pi acos(-1)
#define _(d) while(d(isdigit(ch=getchar())))
using namespace std;
const int N=3005;
LL ans;
int n,num[3],s[3];
struct node{
    int x,y,c;
}t[N];
struct data{
    db v;int c;
    bool operator<(const data&t1)const{
        return v<t1.v;
    }
}f[N<<1];
il int read(){
    int x,f=1;char ch;
    _(!)ch=='-'?f=-1:f;x=ch^48;
    _()x=(x<<1)+(x<<3)+(ch^48);
    return f*x;
}
int main()
{
    n=read();
    for(int i=1;i<=n;i++){
        int x=read(),y=read(),c=read();
        t[i]=(node){x,y,c};s[c]++;
    }
    for(int i=1;i<=n;i++){
        int tot=0;node o=t[i];
        for(int j=1;j<=n;j++)if(i^j)
            f[++tot]=(data){atan2(t[j].y-o.y,t[j].x-o.x),t[j].c};
        sort(f+1,f+1+tot);    
        for(int j=1;j<n;j++)f[++tot]=f[j],f[tot].v+=pi*2.0;
        int now=2;
        for(int j=0;j<3;j++)num[j]=0;
        s[o.c]--;num[f[1].c]++;
        for(int j=1;j<n;j++){
            data g=f[j];
            num[g.c]--;s[g.c]--;
            while(now<=tot&&f[now].v<=g.v+pi){
                num[f[now].c]++;now++;
            }
            LL res1=1,res2=1;
            for(int k=0;k<3;k++)s[k]-=num[k];
            for(int k=0;k<3;k++){
                if(o.c^k)res1*=num[k];
                if(g.c^k)res2*=s[k];
            }
            ans+=res1*res2;
            res1=res2=1;
            for(int k=0;k<3;k++){
                if(o.c^k)res1*=s[k];
                if(g.c^k)res2*=num[k];
            }
            ans+=res1*res2;
            for(int k=0;k<3;k++)s[k]+=num[k];
            s[g.c]++;
        }
        s[o.c]++;
    }
    printf("%lld
",ans>>2);
    return 0;
}