其实,我只会约旦消元法
推荐blog:这里
还有这里(这是高斯)
其实这就是一个小学5年级的数学题-解方程,只是变得有规律可循
具体细节可以先去看看上面的blog,我先说说约旦消元跟高斯消元的区别:
下面是约旦消元消完后的结果,所以它可以不用回带:
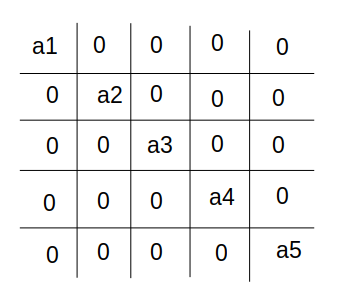
而高斯消元后的结果是这样,所以它还需要从下往上回带:
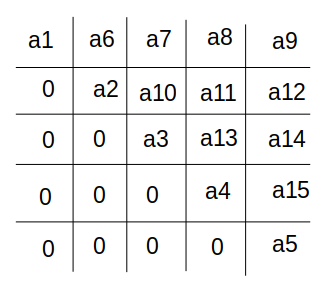
至于怎么消元,就是找到这一列中系数绝对值最大的,然后先将它系数化为1,再分别去别的行,乘以当前行,当前列的系数 ,(整行都乘),然后顺便处理别的列,就做完了
至于为什么要选最大的,第二篇blog有详细说明
推荐题:洛谷P3389 【模板】高斯消元法
代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 double a[105][105],b[105]; 4 int main(){ 5 int n,i,j,Max,k; 6 double can; 7 scanf("%d",&n); 8 for(i=1;i<=n;i++){ 9 for(j=1;j<=n;j++) 10 cin>>a[i][j]; 11 cin>>b[i]; 12 } 13 for(i=1;i<=n;i++){ 14 Max=0; 15 for(j=i;j<=n;j++){ 16 if(fabs(a[j][i])>fabs(a[Max][i]))Max=j; 17 } 18 if(a[Max][i]==0){ 19 printf("No Solution "); 20 return 0; 21 } 22 for(j=i;j<=n;j++){ 23 swap(a[i][j],a[Max][j]); 24 }swap(b[i],b[Max]);//为了保持约旦消元的矩阵队列,从左上到右下有数,其他都为0 25 for(j=1;j<=n;j++){ 26 if(j!=i){ 27 can=a[j][i]/a[i][i]; 28 for(k=i;k<=n;k++){ 29 a[j][k]-=a[i][k]*can; 30 } 31 b[j]-=can*b[i]; 32 }//将a[i][i]先系数化为1,再乘上当前for的a[j][i]的系数(对所有i行的数如此操作) 33 } 34 } 35 for(i=1;i<=n;i++)printf("%.2lf ",b[i]/a[i][i]); 36 return 0; 37 }