LeetCode 52. N皇后 II

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

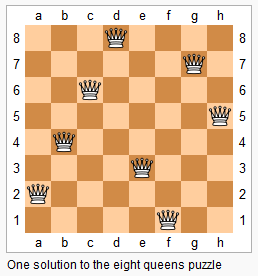
上图为 8 皇后问题的一种解法。

给定一个整数 n，返回 n 皇后不同的解决方案的数量。

示例:

输入: 4
输出: 2
解释: 4 皇后问题存在如下两个不同的解法。
[
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]

class Solution {
public:
    
    int res = 0;
    int size;
    vector<int> path;
    int totalNQueens(int n) {
        size = n;
        for(int i = 0;i < n;++i)
        {
            path.push_back(-1);
        }
        dfs(0);
        return res;
    }
    void dfs(int x)
    {
        if(x == size)
        {
            res++;
        }
        for(int i = 0;i < size; ++i)
        {
            if(check(x,i))
            {
                path[x] = i;
                dfs(x+1);
                path[x] = -1;
            }
        }
    }
    bool check(int x,int k)
    {
        if(x == 0)
            return true;
        for(int i = 0;i < x;i++)
        {
            if(path[i] == k || abs(i - x) == abs(k - path[i]))
            {
                return false;
            }
        }
        return true;
    }


};