概率分析方法与推断统计(来自我写的python书)

    在数据分析统计的场景里，常用的方法除了描述性统计方法外，还有推断统计方法，如果再从工作性质上来划分，推断统计包含了参数估计和假设验证这两方面的内容。而推断统计用到了很多概率统计方法，所以本小节在介绍推断统计的内容前，还将讲述一些常用的概率统计方法。

1 分析收盘价，绘制小提琴图

    小提琴图综合了箱状图与核密度图的特性，从箱状图里能看出数据的各分位数，而从核密度图里，能看出样本数据的分布情况，即每个数值点上样本的密度。

    从统计学的角度来分析，样本密度越大的数值区域，接下来的数据出现在这里的概率也就越大。在如下的ViolinplotDemo.py范例中，将通过matplotlib库的violinplot方法，绘制基于股票收盘价的小提琴图，同时也将对比性地绘制出箱状图，从中大家能直观地理解“核密度”的概念。    

1	import pandas as pd
2	import matplotlib.pyplot as plt
3	filename='D:\work\data\ch9\6007852019-06-012020-01-31.csv'
4	df = pd.read_csv(filename,encoding='gbk',index_col=0)
5	fig = plt.figure()
6	plt.rcParams['font.sans-serif']=['SimHei']
7	axViolin = fig.add_subplot(121)
8	axViolin.violinplot(df['Close'],showmeans=True,showmedians=True)
9	axViolin.set_title('描述收盘价的小提琴图')
10	axViolin.grid(True) 	# 带网格线
11	axBoxplot = fig.add_subplot(122)
12	axBoxplot.boxplot(df['Close'])
13	axBoxplot.set_title('描述收盘价的箱状图')
14	axBoxplot.grid(True) 	# 带网格线
15	plt.show()

    在第4行里，从之前范例准备好的csv文件里得到了股票数据。在第7行和第11行里，通过add_subplot方法，绘制了两个子图。

    在第一个子图里，通过violinplot方法，根据第一个参数df[‘Close’]，绘制了基于股票收盘价的小提琴图，其中showmeans参数表示是否要绘制数据平均线，而showmedians参数则表示是否要绘制数据的中位线，即第50的百分位数。而在第二个子图里，则通过第12行的boxplot方法，绘制基于收盘价的箱状图，上述代码的运行效果如下图所示。

​

    对比左右两个子图，能发现两者的中位线是一致的，而且左边小提琴图里，在约15.4的位置还有一条样本数据平均线的图。此外，小提琴图里，能看到从上往下蓝色区域宽窄不一，宽的区域表示其中样本分布较多，窄的区域则相反，从中能直观地看到收盘价数据的分布情况。

2 用直方图来拟合正态分布效果

    正态分布是一种连续随机变量概率分布，它是很多分析统计方法的基础，比如包括回归分析等在内的多种方法均要求被分析的样本服从正态分布。

    正态分布和直方图相似点在于，它们都能展示变量的分布情况，所以在如下的DrawNormal.py范例中，将先用直方图来拟合正态分布的效果，从中大家能直观地感受到正态分布，随后会再此基础上做进一步分析。    

1	# coding=utf-8
2	import numpy as np
3	import matplotlib.pyplot as plt
4	fig = plt.figure()
5	ax = fig.add_subplot(111)
6	u = 0
7	sigma = 1
8	num = 1000000
9	points = np.random.normal(u, sigma, num)
10	#以直方图来拟合正态分布
11	ax.hist(points, bins=1000)
12	plt.show()

    正态分布有两个关键参数，分别是期望μ和方差为σ^2（即σ的平方），在第6行和第7行里，分别定义这两个关键变量。在第9行里，通过numpy.random.normal方法，以两个关键参数，生成了1000000个符合正态分布的随机数，其中生成的个数有第3个参数num指定。

    在准备好数据后，是通过第11行的hist方法，绘制了描述样本points分布情况的直方图，其中通过bins参数指定了直方图里的柱状图的个数。

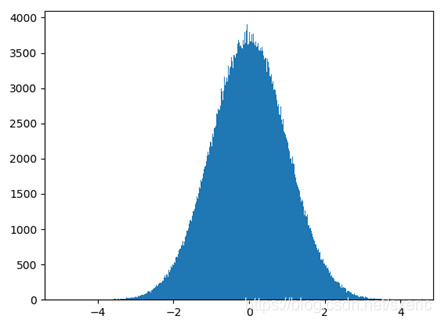
    运行本范例后，能看到如下图9.9所示的效果。从中能看到满足正态分布的随机样本具有如下的特性。

• 正态分布曲线呈钟状，是关于数学期望μ对称，数学期望可以理解成是该随机样本数的平均值，而中间的高度是由方差决定的。
• 从图上能看到这些随机数的分布情况，而0位置的分布最为密集，其中0是生成该正态分布随机数时指定的数学期望值。
• 而且，满足正态分布的随机变量样本集，大约68.3%的样本落在距数学期望值有1个标准差（即σ）的范围内，大约95.4%样本落在在距数学期望值有2个标准差（即2σ）的范围内，大约99.7%样本落在距数学期望值有3个标准差（即3σ）内的范围内。

​

3 验证序列是否满足正态分布

    之前提到，很多数学统计规律和方法是基于正态分布的，也就是说，如果某组样本变量符合正态分布，那么就可以用到这些规律和方法来进行分析或预测工作。那么怎么检验序列是否满足正态分布呢？在scipy.stats模块里封装了normaltest方法，可以用它来检验，在如下的CheckNormal.py范例中，演示了通过该方法的用法。    

1	# coding=utf-8
2	import numpy as np
3	from scipy.stats import normaltest
4	import pandas as pd
5	u = 0
6	sigma = 1
7	num = 1000
8	normalArray = np.random.normal(u, sigma, num)
9	#验证是否是正态分布
10	print(normaltest(normalArray))
11	filename='D:\work\data\ch9\6007852020-01-012020-01-31.csv'
12	df = pd.read_csv(filename,encoding='gbk',index_col=0)
13	print(normaltest(df['Close']))

    在第5行到第8里，指定了期望和方法，生成了1000个随机数，在第10行里，通过normaltest方法验证该序列是否符合正态分布。由于是生成随机数，所以每次结果不会相同，如下给出了其中一次的运行结果。

1. NormaltestResult(statistic=1.9905539749433805, pvalue=0.36962104996359296)

    其中主要看pvalue，从统计学上看，这个数有三档意义，第一档是大于0.05，表示两者差别无显著意义。这里结果约为0.37，符合这一档。该取值在当前上下文中的含义是，该序列和正态分布序列间，差别无显著意义，即normalArray序列符合正态分布， 由于待检验的该序列本身就是以正态分布的方式生成的，所以这个结论无疑是正确的。

    随后在第11行和第12行里，从csv文件里得到股票数据，并用第13行的normaltest方法验证收盘价是否满足正态分布，这行print语句的运行结果如下。

1. NormaltestResult(statistic=4.624089377177887, pvalue=0.09905850056321942)

    虽然pvalue的值0.099比0.05大不了多少，但也能说明股票收盘价的序列满足正态分布。

4 参数估计方法

    参数估计方法是推断统计的一种方法，该方法的理论基础是正态分布，也就是说，如果该方法的适用范围是满足正态分布的序列。参数估计可以再划分成点估计和区间估计，其中点估计的含义是用样本的参数来估计总量中的参数。

    点估计的一个应用场景是抽样检验，其中可以用样本产品的“产品最大工作时间”参数来估计所有产品中的该数值。而区间估计要解决的问题是，根据事先制定的正确度与精确度参数，构造适当的区间范围。通俗地讲，通过区间估计能确定“有多少把握能确保某个样本在某个区间范围内”。

    从上例中已经看到，收盘价是符合正态分布，而且它适用于“区间估计”的场景。在如下的IntervalEst.py范例中，将调用scipy.stats里的interval方法，以95%的置信度，给出该股收盘价的置信区间。   

1	# coding=utf-8
2	from scipy import stats
3	import pandas as pd
4	filename='D:\work\data\ch9\6007852020-01-012020-01-31.csv'
5	df = pd.read_csv(filename,encoding='gbk',index_col=0)
6	print(stats.t.interval(0.95,len(df['Close'])-1,df['Close'].mean(),df['Close'].std()))

    在前5行里，从csv文件里得到了指定股票在指定范围内的数据，在第6行里，通过调用了stats.t.terval方法，计算了df[‘Close’]的置信区间。

    其中第1个参数表示置信度，第2个参数表示自由度，一般是样本数减1，第3个参数一般传入的是均值，第4个参数则表示标准差的计算方式。运行上述范例，能看到如下的输出结果。

1. (14.576210752919142, 16.423789119924283)

    这表示在95%置信度的前提下，该序列的区间范围。

5 显著性验证

    显著性验证是假设验证中的一种。假设验证的思想是，先对样本数据做个假设，然后验证该假设对不对。

    再具体一下，如果原假设是对的，而验证的结果却告诉你要放弃该假设，这叫第一类错误，在假设验证里把第一类错误出现的概率记成α。但如果原假设不对，而结果却要你接收该假设，这叫第二类错误，记作β。

    一般只考虑出现第一类错误的最大概率α，而不考虑出现第二类错误的概率β，这样的假设检验就叫显著性检验，其中出错概率α叫显著性水平。在显著性验证里，α一般的取值有0.05、0.025和0.01这三种，对应地表示出现第一类错误的可能性必须低于5%、2.5%或1%。

    根据样本的概率分布情况，常用的校验方法有t检验、z检验和F检验等，其中通过t检验可以检验服从正态分布的标准差未知的样本序列的均值。在如下的TTestDemo.py范例中，就将演示用t检验验证收盘价的均值。    

1	# coding=utf-8
2	from scipy import stats
3	import pandas as pd
4	filename='D:\work\data\ch9\6007852020-01-012020-01-31.csv'
5	df = pd.read_csv(filename,encoding='gbk',index_col=0)
6	print(df['Close'].mean()) #15.499999936421712
7	print(stats.ttest_1samp(df['Close'],15.5))
8	print(stats.ttest_1samp(df['Close'],15.4))
9	print(stats.ttest_1samp(df['Close'],15.7))
10	print(stats.ttest_1samp(df['Close'],15.2))
11	print(stats.ttest_1samp(df['Close'],16))

    在第6行里，输出了股票收盘价的均值，约为15.5，在第7行到第11行里，提出了不同的关于收盘价均值的假设，并通过stats模块里的ttest_lsamp方法，对不同的假设进行了t检验。上述范例运行后的结果如下所示。    

1	15.499999936421712
2	Ttest_1sampResult(statistic=-5.716967037005381e-07, pvalue=0.9999995519184666)
3	Ttest_1sampResult(statistic=0.8992005958223217, pvalue=0.38375142019051156)
4	Ttest_1sampResult(statistic=-1.7984029067347544, pvalue=0.09370333462557079)
5	Ttest_1sampResult(statistic=2.6976029308603886, pvalue=0.017337840975255838)
6	Ttest_1sampResult(statistic=-4.496006409291847, pvalue=0.0005030226952314426)

     上述输出结果的第1行表示序列的均值，从第2行到第6行的pvalue结果里，能看到对不同假设的验证结果，详细说明请参考下表里的内容。

待校验的均值	与正确均值的偏差	pvalue的取值
15.5	约为0	接近于1
15.4	约0.1	约0.38
15.7	约0.2	约0.09
15.2	约0.3	约0.01
16	约0.5	约0.0005

    也就是说，如果待验证的均值越接近于真实的均值，那么pvalue的取值就越高，说明“该数值是正确均值”的假设成立的可能性就越高，反之pvalue取值就很低，比如针对“均值是16”的假设，成立的概率才约0.0005，就说明该假设基本不成立。

本文出自我写的书： Python爬虫、数据分析与可视化：工具详解与案例实战，https://item.jd.com/10023983398756.html

    ​

    请大家关注我的公众号：一起进步，一起挣钱，在本公众号里，会有很多精彩文章。

​