数据结构之二叉树

数据结构分线性存储结构和非线性存储结构，前面说的顺序表，单链表，双链表，栈，队列都属于线性结构，线性结构的特别是集合中必存在唯一的一个"第一个元素，集合中必存在唯一的一个"最后的元素"；除最后元素之外，其它数据元素均有唯一的"后继"；除第一元素之外，其它数据元素均有唯一的"前驱"。大家注意的是唯一2个字，也就是说线性结构不可能存在2个或多个前驱结点，同样不可能出现2个或多个后继结点，现在我们说下2叉树，很明显是非线性的因为它有2个后继结点。

一：树的基本概念

父母结点：结点的前驱节点称为父母结点

孩子结点：结点的后继节点称为孩子结点

兄弟结点：拥有同一父母的结点称为兄弟结点

度：结点拥有子树的的个数（后继节点的个数）没有后继结点的称为叶子结点（树的度指的是所有结点中度最大的）

结点层次：指的是按照这个结点算起来的高度。

树的高度：就是树的层次。

二：二叉树结点类

public class BinaryNode<T> {
    public T data;
    public BinaryNode<T> left;
    public BinaryNode<T> right;

    public BinaryNode(T data, BinaryNode<T> left, BinaryNode<T> right) {
        this.data = data;
        this.left = left;
        this.right = right;
    }

    public BinaryNode(T data) {//构建叶子节点
        this(data, null, null);
    }

    public BinaryNode() {
        this(null, null, null);
    }
}

 三：树的抽象接口

public interface BinaryTTree<T> {
    /**
     * 判断二叉树是否为null
     * @return
     */
    boolean isEmpty();

    /**
     * 返回二叉树节点个数
     * @return
     */
    int count();

    /**
     * 返回二叉树的高度
     * @return
     */
    int height();

    /**
     * 先根遍历
     */
    void preOrder();

    /**
     * 中根遍历
     */
    void inOrder();

    /**
     * 后跟遍历
     */
    void postOrder();

    /**
     * 层次遍历
     */
    void levelOrder();

    /**
     * 查找并返回首次出现关键字为key的元素节点
     * @param key
     * @return
     */
    BinaryNode<T> search(T key);

    /**
     * 返回弄得节点的父节点
     * @param node
     * @return
     */
    BinaryNode<T> getParent(BinaryNode<T> node);

    /**
     * 插入x作为根节点
     * @param x
     */
    void insertRoot(T x);

    /**
     * 插入p的孩子节点（leftchild验证为左子树还是右子树）
     * @return
     */
    BinaryNode<T> insertChild(BinaryNode<T> p,T x,boolean leftChild);

    /**
     * 删除p节点的左或者右子树
     * @param p
     * @param leftChild
     */
    void removeChild(BinaryNode<T> p,boolean leftChild);

    /**
     * 删除二叉树
     */
    void removeAll();
}

四：树的实现

现在我先画一个很简单的树来帮助理解

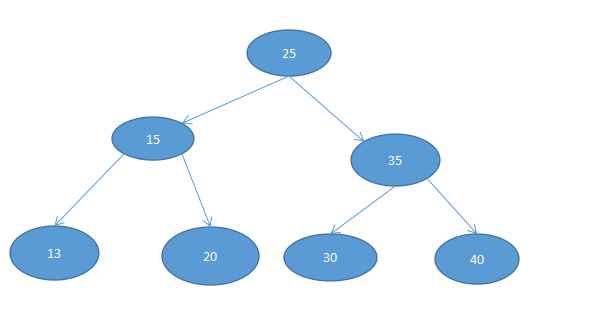
首先我们应该定义一个根，如果这个根空，则表示是空树。比如上面这颗树我们怎么计算他结点的个数呢，我们采取的方式是计算左子树的个数+右子树的个数+根不就是么，我们采用递归的思想来解决。

 public int count() {
        return count(this.root);
    }
    private int count(BinaryNode<T> node){
        if (node==null){
            return 0;
        }
        return 1+count(node.left)+count(node.right);
    }

二叉树的高度其实道理一样，计算左子树高度和右子树高度取大的然后加上根即可

 public int height() {
        return height(this.root);
    }

    public int height(BinaryNode<T> root) {
        if (root == null) {
            return 0;
        }
        int lh = height(root.left);
        int rh = height(root.right);
        return lh >= rh ? lh + 1 : rh + 1;
    }

先根遍历，就是先遍历根然后左子树然后右子树，比如上面的采用先根就是25,15,13,20,35，30,40.代码如下

  public void preOrder() {
        System.out.println("先根遍历开始：");
        preOrder(this.root);
        System.out.println();
    }
    public void preOrder(BinaryNode<T> p){
        if (p!=null){
            System.out.println(p.data.toString()+" ");
            preOrder(p.left);
            preOrder(p.right);
        }
    }

中根是先执行左子树然后根最后右子树

 public void inOrder() {
        System.out.println("中根遍历开始：");
        inOrder(this.root);
        System.out.println();
    }

    public void inOrder(BinaryNode<T> p){
        if (p!=null){
            inOrder(p.left);
            System.out.println(p.data.toString()+" ");
            inOrder(p.right);
        }
    }

后根是先左子树，然后右子树最后才根

public void postOrder() {
        System.out.println("后跟遍历");
        postOrder(this.root);
        System.out.println();
    }
    public void postOrder(BinaryNode<T> p){
        if (p!=null){
            postOrder(p.left);
            postOrder(p.right);
            System.out.println(p.data.toString()+" ");
        }
    }

查找也是如何，先从根比对，然后比对多有的左子树，如果没有找到在从右子树中查找

public BinaryNode<T> search(T key) {
        return search(this.root, key);
    }

    public BinaryNode<T> search(BinaryNode<T> node,T key) {
        if (node == null || key == null) {
            return null;
        }
        if (node.data.equals(key)) {
            return node;
        }
        BinaryNode<T> find = search(node.left, key);
        if (find == null) {
            find = search(node.right, key);
        }
        return find;
    }

 public BinaryNode<T> getParent(BinaryNode<T> node) {
       if (this.root==null||node==null||this.root==node){
           return null;
       }
        return getParent(this.root,node);
    }
    //以p为根的子树中查找，并返回node节点的父母节点
    public BinaryNode<T> getParent(BinaryNode<T> p,BinaryNode<T> node){
        if (p.left==node||p.right==node){
            return p;
        }
        BinaryNode<T> find=getParent(p.left,node);
        if (find==null){
            find=getParent(p.right,node);
        }
        return find;
    }

    public void insertRoot(T x) {
        this.root = new BinaryNode<T>(x, this.root, null);
    }


    public BinaryNode<T> insertChild(BinaryNode<T> p, T x, boolean leftChild) {
        if (p==null||x==null){
            return null;
        }
        if (leftChild){
            p.left=new BinaryNode<T>(x,p.left,null);
            return p.left;
        }
        p.right=new BinaryNode<T>(x,null,p.right);
        return p.right;
    }

    public void removeChild(BinaryNode<T> p, boolean leftChild) {
        if (p != null) {
            if (leftChild) {
                p.left = null;
            } else {
                p.right = null;
            }
        }
    }

    public void removeAll() {
        this.root=null;
    }

五：排序二叉树

主要说二叉树的添加和删除

首先第一步必须找到要插入节点的位置，也就是说找到这个即将插入这个结点的父结点

    if (this.root == null) {
            this.root = new BinaryNode<T>(x);
        } else {
            BinaryNode<T> p = this.root, parent = null;
            while (p != null) {
                parent = p;
                if (x.compareTo(p.data) == 0) {
                    return;
                }
                if (x.compareTo(p.data) < 0) {
                    p = p.left;
                }else {
                    p=p.right;
                }
            }

我们先分析这段代码，如果是空树就和简单直接赋值即可，如果非空，我们分别申明2个变量，用parent来记录父结点，我们知道我们要插入的树已经是顺序的了，所以我们只要知道这个要插入的节点放在左边还是右边。我们找到了这个节点的父结点了就好办了。我们只需要和父结点比对即可，如果小就是左子树，如果打就是右子树

  p = new BinaryNode<T>(x);
            if (x.compareTo(parent.data) <= 0) {
                parent.left = p;
            } else {
                parent.right = p;
            }

删除是相对比较复杂的，但是同样首先要找到要删除的结点p，然后在进行操作如下

  if (p==null){
            return null;
        }
        //首先找到删除节点p
        if (x.compareTo(p.data)<0){
            return remove(x,p.left,p);
        }
        if (x.compareTo(p.data)>0){
            return remove(x,p.right,p);
        }

现在有几种情况，第一这个父结点左子树为null右子树不为null；第二右子树为null左子树不为null，第三都不为null。第一种情况我们只需要把要删除的p结点替换它的右子树即可，第二种情况我们同样把删除的p结点替换成它的左子树。第三种情况，既然删除父结点p我们只要需要把p结点的右子树中最小的结点赋值给这个删除的p结点即可，然后置空p结点右子树中的最小结点

 if (p.left!=null&&p.right!=null){
            BinaryNode<T> insucc=p.right;
            while (insucc.left!=null){
                insucc=insucc.left;
            }//找到要删除节点的节点
            p.data=insucc.data;
            return remove(p.data,p.right,p);
        }

然后我们考虑一下特别情况，比如这颗树 本身是叶子结点，或者度为1，那么直接进行转换就可以

if (parent==null){
            if (p.left!=null){
                root=p.left;
            }else {
                root=p.right;
            }
            return p;
        }

最后代码如下

if (p==parent.left){
            if (p.left!=null){
                parent.left=p.left;
            }else {
                parent.left=p.right;
            }
        }else {
            if (p.left!=null){
                parent.right=p.left;
            }else {
                parent.right=p.right;
            }
        }