牛客网暑期ACM多校训练营（第六场） C Generation I(组合数学， 逆元)

中链接：

https://www.nowcoder.com/acm/contest/144/C

题意：

给定n个集合， 要求用n次操作， 第i次操作用1~m中一个数填入 i ~ n个集合中， 集合无序而且元素不重复。

分析：

因为要填入i ~ n个集合中， 所以考虑最后一个集合， 其实每个数只有第一次出现才是有效的， 假设有k个数出现（我们可以枚举这个k）， 那么这k个数的排列就是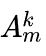

因为第一个数是不会有影响的， 所以可以把k个数的第一个放到第一位。

剩下的（k-1）个数要放进（n-1）个格子中有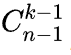种方法， 其实这些位置就是这个数第一次出现的位置， 剩余n-k的位置其实是没有贡献的。

答案就是

拆开看第k项就是

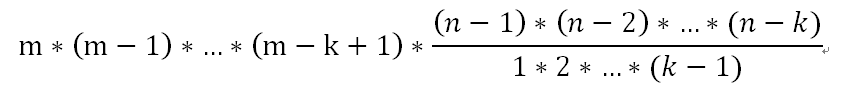
那么可以从k = 1递推， 

特殊地ans[1] = m

ans[2] = ans[1] * (m-1) * (n-1) / 1

ans[3] = ans[2] * (m-2) * (n-2) / 2...

注意求模跟逆元就行了

#include<bits/stdc++.h>
using namespace std;
const long long MOD = 998244353;
const int maxN = 1e6;
long long inv(long long a, long long b){
    long long sum = 1;
    while(b){
        if(b & 1) sum = sum * a % MOD;
        b /= 2;
        a = a * a % MOD;
    }
    return sum;
}
long long n, m, Min;
long long Inv[maxN + 1123]; //a() c(n,m)
void init() {
    Inv[1] = 1;
    long long _ = 1;
    for(int i = 2; i <= maxN; i++){
        Inv[i] = inv(i, MOD - 2);
    }
}
int main() {
    init();
    int T;
    scanf("%d", &T);
    for(int kase = 1; kase <= T; kase++) {
        scanf("%lld %lld",&n , &m);
        Min = min(n, m);
  
        m %= MOD, n %= MOD;
  
        long long ans = m;
        long long sum = m;
        for(int i = 1; i < Min; i++){
            sum = sum * (m - i) % MOD * (n - i) % MOD * Inv[i] % MOD;
            ans += sum;
            ans %= MOD;
        }
        printf("Case #%d: %lld
",kase,  ans);
    }
}