| Time Limit: 12000MS | Memory Limit: 65536K | |
| Total Submissions: 58002 | Accepted: 16616 | |
| Case Time Limit: 5000MS | ||
An array of size n ≤ 106 is given to you. There is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves rightwards by one position. Following is an example:
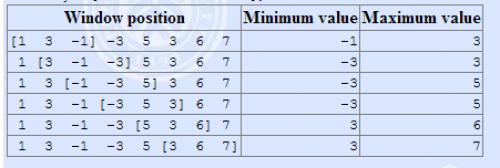
The array is [1 3 -1 -3 5 3 6 7], and k is 3.
The array is [1 3 -1 -3 5 3 6 7], and k is 3.
| Window position | Minimum value | Maximum value |
|---|---|---|
| [1 3 -1] -3 5 3 6 7 | -1 | 3 |
| 1 [3 -1 -3] 5 3 6 7 | -3 | 3 |
| 1 3 [-1 -3 5] 3 6 7 | -3 | 5 |
| 1 3 -1 [-3 5 3] 6 7 | -3 | 5 |
| 1 3 -1 -3 [5 3 6] 7 | 3 | 6 |
| 1 3 -1 -3 5 [3 6 7] | 3 | 7 |
Your task is to determine the maximum and minimum values in the sliding window at each position.
Input
The input consists of two lines. The first line contains two integers n and k which are the lengths of the array and the sliding window. There are n integers in the second line.
Output
There are two lines in the output. The first line gives the minimum values in the window at each position, from left to right, respectively. The second line gives the maximum values.
Sample Input
8 3 1 3 -1 -3 5 3 6 7
Sample Output
-1 -3 -3 -3 3 3 3 3 5 5 6 7
Source
POJ Monthly--2006.04.28, Ikki
题目描述
现在有一堆数字共N个数字(N<=10^6),以及一个大小为k的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。
例如:
The array is [1 3 -1 -3 5 3 6 7], and k = 3.
输入输出格式
输入格式:
输入一共有两行,第一行为n,k。
第二行为n个数(<INT_MAX).
输出格式:
输出共两行,第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值
输入输出样例
输入样例#1:
8 3 1 3 -1 -3 5 3 6 7
输出样例#1:
-1 -3 -3 -3 3 3 3 3 5 5 6 7
说明
50%的数据,n<=10^5
100%的数据,n<=10^6
思路:单调队列。
分别维护一个单调上升队列和一个单调下降队列即可。
拿区间最大值来说吧,一个上升队列,它的队首值就是区间最大值。
如果窗口向后滑动,首先,在满足队列单调的前提下,把新值加入(不一定真的加入)。
如果队首值等于要去掉的值,队首后移。
代码实现:
1 #include<cstdio> 2 #define maxn 1000010 3 int n,k,s[maxn]; 4 int a; 5 int h1,t1,q1[maxn],a1[maxn],l1; 6 int h2,t2,q2[maxn],a2[maxn],l2; 7 int main(){ 8 scanf("%d%d",&n,&k); 9 for(int i=1;i<=n;i++){ 10 scanf("%d",&s[i]); 11 a=h1-1;h1=t1; 12 for(int j=a;j>=t1;j--) if(s[i]>=q1[j]){h1=j+1;break;} 13 q1[h1++]=s[i]; 14 if(i>k&&s[i-k]==q1[t1]) t1++;//因为判断先后的问题,一直RE一个点。 15 if(i>=k) a1[l1++]=q1[t1]; 16 a=h2-1;h2=t2; 17 for(int j=a;j>=t2;j--) if(s[i]<=q2[j]){h2=j+1;break;} 18 q2[h2++]=s[i]; 19 if(i>k&&s[i-k]==q2[t2]) t2++; 20 if(i>=k) a2[l2++]=q2[t2]; 21 } 22 for(int i=0;i<l1;i++) printf("%d ",a1[i]);putchar(' '); 23 for(int i=0;i<l2;i++) printf("%d ",a2[i]);putchar(' '); 24 return 0; 25 }
另一种写法(更工整些):
1 #include<cstdio> 2 #define maxn 1000010 3 int n,k,s[maxn]; 4 int a; 5 int h1,t1,q1[maxn],a1[maxn],l1; 6 int h2,t2,q2[maxn],a2[maxn],l2; 7 int main(){ 8 scanf("%d%d",&n,&k); 9 for(int i=1;i<=n;i++){ 10 scanf("%d",&s[i]); 11 q1[h1++]=1000000000;q2[h2++]=-1000000000; 12 for(int j=t1;j<h1;j++) 13 if(s[i]<q1[j]){q1[j]=s[i];h1=j+1;break;} 14 if(i>k&&s[i-k]==q1[t1]) t1++; 15 if(i>=k) a1[l1++]=q1[t1]; 16 for(int j=t2;j<h2;j++) 17 if(s[i]>q2[j]){q2[j]=s[i];h2=j+1;break;} 18 if(i>k&&s[i-k]==q2[t2]) t2++; 19 if(i>=k) a2[l2++]=q2[t2]; 20 } 21 for(int i=0;i<l1;i++) printf("%d ",a1[i]);putchar(' '); 22 for(int i=0;i<l2;i++) printf("%d ",a2[i]);putchar(' '); 23 return 0; 24 }
也可以分开写:
1 #include<cstdio> 2 #define maxn 1000010 3 int n,k,a,h,t; 4 int s[maxn],q[maxn]; 5 int main(){ 6 scanf("%d%d",&n,&k); 7 for(int i=1;i<=n;i++){ 8 scanf("%d",&s[i]); 9 q[h++]=1000000000; 10 for(int j=t;j<h;j++) if(s[i]<q[j]){q[j]=s[i];h=j+1;break;} 11 if(i>k&&s[i-k]==q[t]) t++; 12 if(i>=k) printf("%d ",q[t]); 13 } 14 putchar(' ');h=t=0; 15 for(int i=1;i<=n;i++){ 16 q[h++]=-1000000000; 17 for(int j=t;j<h;j++) if(s[i]>q[j]){q[j]=s[i];h=j+1;break;} 18 if(i>k&&s[i-k]==q[t]) t++; 19 if(i>=k) printf("%d ",q[t]); 20 } 21 putchar(' '); 22 return 0; 23 }
越来越短。
最后被poj G++接受的代码(2266mm):
1 #include<cstdio> 2 #define maxn 1000010 3 int n,k,s[maxn]; 4 int a; 5 int h1,t1,q1[maxn],a1[maxn],l1; 6 int h2,t2,q2[maxn],a2[maxn],l2; 7 inline int abs(int x){return x<0?-x:x;} 8 void write(int x){ 9 if(x) write(x/10); 10 else return; 11 putchar(x%10+'0'); 12 } 13 int main(){ 14 scanf("%d%d",&n,&k); 15 for(int i=1;i<=n;i++){ 16 scanf("%d",&s[i]); 17 a=h1-1;h1=t1; 18 for(int j=a;j>=t1;j--) if(s[i]>=q1[j]){h1=j+1;break;} 19 q1[h1++]=s[i]; 20 if(i>k&&s[i-k]==q1[t1]) t1++; 21 if(i>=k) a1[l1++]=q1[t1]; 22 a=h2-1;h2=t2; 23 for(int j=a;j>=t2;j--) if(s[i]<=q2[j]){h2=j+1;break;} 24 q2[h2++]=s[i]; 25 if(i>k&&s[i-k]==q2[t2]) t2++; 26 if(i>=k) a2[l2++]=q2[t2]; 27 } 28 for(int i=0;i<l1;i++){ 29 if(a1[i]<0) putchar('-'); 30 write(abs(a1[i])); 31 if(!a1[i]) putchar('0'); 32 if(i<l1-1) putchar(' '); 33 } 34 putchar(' '); 35 for(int i=0;i<l2;i++){ 36 if(a2[i]<0) putchar('-'); 37 write(abs(a2[i])); 38 if(!a2[i]) putchar('0'); 39 if(i<l2-1) putchar(' '); 40 } 41 putchar(' '); 42 return 0; 43 }
除了最后一个 G++ 格式都T了,C++却能A,不知道为什么。
洛谷70分T掉的线段树
1 #include<cstdio> 2 const int maxn=4e6; 3 int n,k; 4 int s[maxn]; 5 int t_min[maxn],t_max[maxn]; 6 inline int min_(int x,int y){return x<y?x:y;} 7 inline int max_(int x,int y){return x>y?x:y;} 8 void build_min(int k,int l,int r){ 9 if(l==r){ 10 t_min[k]=s[l]; 11 return; 12 } 13 int mid=l+r>>1,ls=k<<1,rs=ls|1; 14 build_min(ls,l,mid); 15 build_min(rs,mid+1,r); 16 t_min[k]=t_min[ls]<t_min[rs]?t_min[ls]:t_min[rs]; 17 } 18 int search_min(int k,int l,int r,int al,int ar){ 19 if(al==l&&ar==r) return t_min[k]; 20 int ret=1e9,mid=l+r>>1,ls=k<<1,rs=ls|1; 21 if(al<=mid) ret=min_(ret,search_min(ls,l,mid,al,min_(ar,mid))); 22 if(ar>mid) ret=min_(ret,search_min(rs,mid+1,r,max_(al,mid+1),ar)); 23 return ret; 24 } 25 void build_max(int k,int l,int r){ 26 if(l==r){ 27 t_max[k]=s[l]; 28 return; 29 } 30 int mid=l+r>>1,ls=k<<1,rs=ls|1; 31 build_max(ls,l,mid); 32 build_max(rs,mid+1,r); 33 t_max[k]=t_max[ls]>t_max[rs]?t_max[ls]:t_max[rs]; 34 } 35 int search_max(int k,int l,int r,int al,int ar){ 36 if(al==l&&ar==r) return t_max[k]; 37 int ret=-1e9,mid=l+r>>1,ls=k<<1,rs=ls|1; 38 if(al<=mid) ret=max_(ret,search_max(ls,l,mid,al,min_(ar,mid))); 39 if(ar>mid) ret=max_(ret,search_max(rs,mid+1,r,max_(al,mid+1),ar)); 40 return ret; 41 } 42 int main(){ 43 scanf("%d%d",&n,&k); 44 for(int i=1;i<=n;i++) scanf("%d",&s[i]); 45 build_min(1,1,n); 46 build_max(1,1,n); 47 for(int i=1;i<=n-k+1;i++) 48 printf("%d ",search_min(1,1,n,i,i+k-1)); 49 putchar(' '); 50 for(int i=1;i<=n-k+1;i++) 51 printf("%d ",search_max(1,1,n,i,i+k-1)); 52 putchar(' '); 53 return 0; 54 }
常数优化十分可观的zkw线段树(洛谷 2275ms)
1 #include<cstdio> 2 const int maxn=1<<22; 3 int n,k,m; 4 int t[maxn]; 5 inline int min_(int x,int y){return x<y?x:y;} 6 inline int max_(int x,int y){return x>y?x:y;} 7 void build_min(){for(int i=m-1;i>0;i--) t[i]=min_(t[i<<1],t[i<<1|1]);} 8 int search_min(int l,int r,int ret){ 9 for(l+=m,r+=m;r-l!=1;l>>=1,r>>=1){ 10 if(~l&1) ret=min_(ret,t[l^1]); 11 if(r&1) ret=min_(ret,t[r^1]); 12 } 13 return ret; 14 } 15 void build_max(){for(int i=m-1;i>0;i--) t[i]=max_(t[i<<1],t[i<<1|1]);} 16 int search_max(int l,int r,int ret){ 17 for(l+=m,r+=m;r-l!=1;l>>=1,r>>=1){ 18 if(~l&1) ret=max_(ret,t[l^1]); 19 if(r&1) ret=max_(ret,t[r^1]); 20 } 21 return ret; 22 } 23 int main(){ 24 scanf("%d%d",&n,&k); 25 for(m=1;m<=n+1;m<<=1); 26 for(int i=1;i<=n;i++) scanf("%d",t+m+i); 27 build_min(); 28 for(int i=0;i<=n-k;i++) 29 printf("%d ",search_min(i,i+k+1,1e9)); 30 putchar(' '); 31 build_max(); 32 for(int i=0;i<=n-k;i++) 33 printf("%d ",search_max(i,i+k+1,-1e9)); 34 putchar(' '); 35 return 0; 36 }
题目来源:POJ,洛谷