

分析:
首先考虑\(dp\),设\(f_{i,j}\)表示\(A\)用了前\(i\)个,\(B\)用了前\(j\)个的方案数
先给出式子:
\[f_{i,j}=f_{i-1,j}+f_{i,j-1}-\sum_{A_{i-k...i}==B_{j-k...j}}f_{i-k-1,j-k-1}Cat_{k}
\]
求和下面的条件是\(A\)和\(B\)的某一段相同,\(Cat\)是卡特兰数
如果没有同样的颜色,不用后面的求和,算出来的答案就是正确的,但是有了同样的颜色,前面的会算重
后面的求和相当于两个相同的长度为\(k+1\)的序列能排出多少种不同的序列
想象成在\((k+1)*(k+1)\)的格子的轮廓线上走,选一个\(A\)就向右走一步,选一个\(B\)就向下走一步
假设其中一条路径是这样:
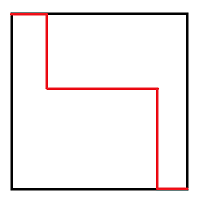
我们沿对角线翻折:
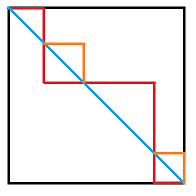
红色路径翻折后得到的橙色路径形成的字符串是相同的
本来的路径数是\(\binom{2k+2}{k+1}\),形成的本质不同的字符串为\(Cat_{k+1}\)种
所以多出来的为\(\binom{2k+2}{k+1}-Cat_{k+1}=Cat_k\)种
总复杂的\(O(n^2)\)
(数据很水,后面的求和不乘卡特兰数的系数有90分,我的k++写成了k--有50分23333
(只有一半的数据最长公共子串长度大于1??只有一个点最长公共子串长度大于2??看来数据是随机的2333
#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#include<vector>
#include<string>
#define maxn 2005
#define INF 0x3f3f3f3f
#define MOD 998244353
using namespace std;
inline int getint()
{
int num=0,flag=1;char c;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
return num*flag;
}
int n;
int f[maxn][maxn];
int a[maxn],b[maxn],Cat[maxn];
int main()
{
n=getint();
for(int i=1;i<=n;i++)a[i]=getint();
for(int i=1;i<=n;i++)b[i]=getint();
Cat[0]=1;
for(int i=1;i<=n;i++)for(int j=0;j<i;j++)Cat[i]=(Cat[i]+1ll*Cat[j]*Cat[i-j-1])%MOD;
f[0][0]=1;
for(int i=0;i<=n;i++)for(int j=0;j<=n;j++)
{
if(i)f[i][j]=(f[i][j]+f[i-1][j])%MOD;
if(j)f[i][j]=(f[i][j]+f[i][j-1])%MOD;
int k=0;
while(i-k>0&&j-k>0&&a[i-k]==b[j-k])f[i][j]=(f[i][j]-1ll*f[i-k-1][j-k-1]*Cat[k]%MOD+MOD)%MOD,k++;
}
printf("%d\n",f[n][n]);
}
