[Noip2007]Core树网的核

Time Limit: 10 Sec  Memory Limit: 64 MB
Submit: 2465  Solved: 830
[Submit][Status][Discuss]

Description

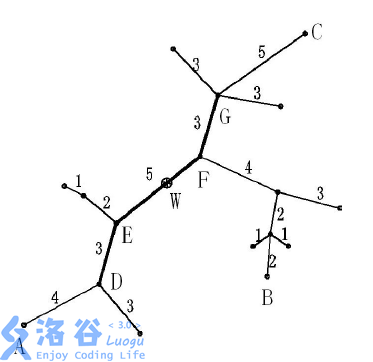
设T=(V, E, W) 是一个无圈且连通的无向图（也称为无根树），每条边带有正整数的权，我们称T为树网（treenetwork），其中V, E分别表示结点与边的集合，W表示各边长度的集合，并设T有n个结点。 路径：树网中任何两结点a,b都存在唯一的一条简单路径，用d(a,b)表示以a,b为端点的路径的长度，它是该路径上各边长度之和。我们称d(a,b)为a,b两结点间的距离。 一点v到一条路径P的距离为该点与P上的最近的结点的距离： d(v，P)=min{d(v，u)，u为路径P上的结点}。 树网的直径：树网中最长的路径称为树网的直径。对于给定的树网T，直径不一定是唯一的，但可以证明：各直径的中点（不一定恰好是某个结点，可能在某条边的内部）是唯一的，我们称该点为树网的中心。 偏心距ECC(F)：树网T中距路径F最远的结点到路径F的距离，即 。 任务：对于给定的树网T=(V, E,W)和非负整数s，求一个路径F，它是某直径上的一段路径（该路径两端均为树网中的结点），其长度不超过s（可以等于s），使偏心距ECC(F)最小。我们称这个路径为树网T=(V,E,W)的核（Core）。必要时，F可以退化为某个结点。一般来说，在上述定义下，核不一定只有一个，但最小偏心距是唯一的。 下面的图给出了树网的一个实例。图中，A-B与A-C是两条直径，长度均为20。点W是树网的中心，EF边的长度为5。如果指定s=11，则树网的核为路径DEFG（也可以取为路径DEF），偏心距为8。如果指定s=0（或s=1、s=2），则树网的核为结点F，偏心距为12。

 

下面的图给出了树网的一个实例。图中，$A-B$与$A-C$是两条直径，长度均为$20$。点$W$是树网的中心，$EF$边的长度为$5$。如果指定$s=11$，则树网的核为路径DEFG（也可以取为路径DEF），偏心距为$8$。如果指定$s=0$（或$s=1$、$s=2$），则树网的核为结点$F$，偏心距为$12$。

Input

包含n行： 第1行，两个正整数n和s，中间用一个空格隔开。其中n为树网结点的个数，s为树网的核的长度的上界。设结点编号依次为1, 2, ..., n。 从第2行到第n行，每行给出3个用空格隔开的正整数，依次表示每一条边的两个端点编号和长度。例如，“2 4 7”表示连接结点2与4的边的长度为7。 所给的数据都是正确的，不必检验。

Output

只有一个非负整数，为指定意义下的最小偏心距。

Sample Input

5 2
1 2 5
2 3 2
2 4 4
2 5 3

Sample Output

5

HINT

对于70%的数据，n<=200000
对于100%的数据：n<=500000, s<2^31, 所有权值<500

==============================================
似乎SPOJ上加强版的数据...

简单来说就是在最长直径上，维护一段小于s的路径F，使得偏心距最小

首先明确几个性质：

1、维护路径F的长度s越长越好

2、最小偏心距的端点，要么存在于直径的端点，要么存在于最大深度的点

性质1显然成立

现在证明性质2：

以上图为例，假设树网的核为结点C，如果最小偏心距为B的话，那么C-B就会成为直径，而从图上看显然不成立

先写一遍bfs，莫名WA了，后改成了dfs

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

const int MAXN=1000000;
const int INF=0x7f7f7f7f;

struct Edge
{
    int to,w,next;
}E[MAXN];
int node,head[MAXN];
int n,s,ans=INF;
int f[MAXN],dis[MAXN];
bool mk[MAXN];

void insert(int u,int v,int w)
{
    E[++node]=(Edge){v,w,head[u]};head[u]=node;
    E[++node]=(Edge){u,w,head[v]};head[v]=node;
}

void dfs(int u,int fa)
{
    f[u]=fa;
    for(int i=head[u];i;i=E[i].next)
    {
        if(E[i].to==fa||mk[E[i].to]) continue;
        dis[E[i].to]=dis[u]+E[i].w;
        dfs(E[i].to,u);
    }
}

int main()
{
    scanf("%d%d",&n,&s);
    for(int i=1;i<n;i++)
    {
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        insert(u,v,w);
    }
    int l=1,r=1;
    dfs(1,0);
    for(int i=1;i<=n;i++)
        if(dis[i]>dis[l]) l=i;
    dis[l]=0;
    dfs(l,0);
    for(int i=1;i<=n;i++)
        if(dis[i]>dis[r]) r=i;
    for(int i=r,j=r;i;i=f[i])
    {
        while(f[j]&&dis[i]-dis[f[j]]<=s) j=f[j];
        ans=min(ans,max(dis[j],dis[r]-dis[i]));
    }
    for(int i=r;i;i=f[i]) mk[i]=1;
    for(int i=r;i;i=f[i])
    {
        dis[i]=0;
        dfs(i,f[i]);
    }
    for(int i=1;i<=n;i++)
        ans=max(ans,dis[i]);
    printf("%d",ans);
    return 0;
}