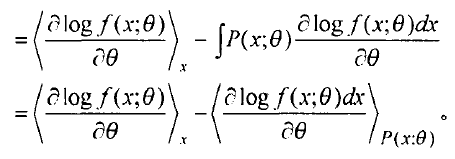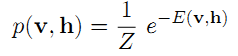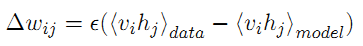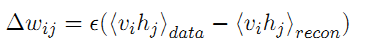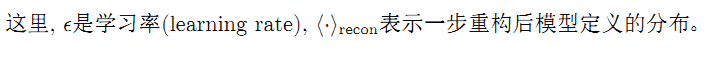受限波尔兹曼网络RBM是一个双层网络:可见层和隐含层。
1. 概述
前面描述的神经网络模型是一种确定的结构。而波尔兹曼网络是一种随机网络。如何来描述一个随机网络呢?很多书上有大量的篇幅介绍其原理。这里把它总结为以下两点。
第一,概率分布函数。由于网络节点的取值状态是随机的,从贝叶斯网的观点来看,要描述整个网络,需要用三种概率分布来描述系统。即联合概率分布(多个条件同时满足的概率),边缘概率分布(高维变量中的低维变量的分布)和条件概率分布。要搞清楚这三种不同的概率分布,是理解随机网络的关键,这里向大家推荐的书籍是张连文所著的《贝叶斯网引论》。很多文献上说受限波尔兹曼是一个无向图,这一点也有失偏颇。从贝叶斯网的观点看,受限波尔兹曼网应该是一个双向的有向图。即从输入层节点可以计算隐层节点取某一种状态值的概率,反之亦然.
第二,能量函数。随机神经网络是根植于统计力学的。受统计力学中能量泛函的启发,引入了能量函数。能量函数是描述整个系统状态的一种测度。系统越有序或者概率分布越集中,系统的能量越小。反之,系统越无序或者概率分布越趋于均匀分布,则系统的能量越大。能量函数的最小值,对应于系统的最稳定状态。(好比社会里面,阶级分明会更稳定)
2. 网络结构和学习算法
2.1 RBM网络结构如下:
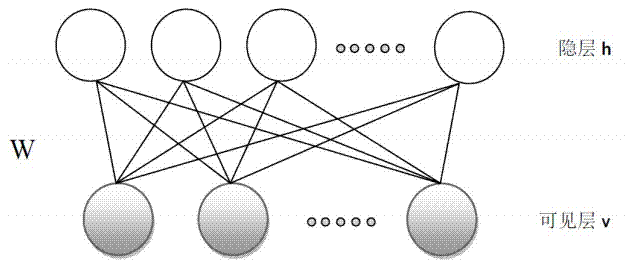
正如前面我们提到的,描述RBM的方法是能量函数和概率分布函数。实际上,把它们二者结合起来,也就是概率分布是能量函数的泛函(从函数空间到数域的映射),其能量泛函和联合概率分布如下:
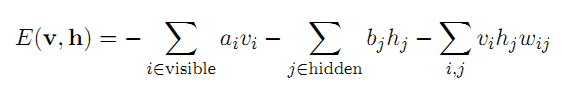
其中,上式中的Z是归一化系数,它的定义如下:
而输入层的边缘概率,是我们感兴趣的,它的计算如下:

因为,网络学习的目的是最大可能的拟合输入数据。根据极大似然学习法则,我们的目的就是对所以的输入,极大化上面的公式(4)(已经出现的是最可能出现的),公式4在统计学里也称作似然函数,更多的我们对其取对数,也就是对数似然函数,考虑所有的输入样本,其极大化对数似然函数的定义如下: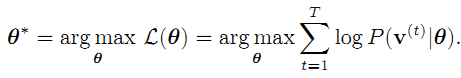
注意,上面的公式中,多了个theta。theta就是网络的权值,包括公式(1)中的w,a,b,是网络学习需要优化的参数。其实在上面所有的公式中都有theta这个变量,只是为了便于描述问题,我把它们都给抹掉了。
2.2 对比度散度学习算法
根据公式5,逐步展开,运用梯度下降策略,可以推导出网络权值的更新策略如下:
其中,第一项,是给定样本数据的期望,第二项是模型本身的期望。数据的期望,很容易计算,而模型的期望不能直接得到。一种典型的方法是通过吉布斯采样得到,而Hinton提出了一种快速算法,称作contrastive divergence算法。这种算法只需迭代k次,就可以获得对模型的估计,而通常k等于1. CD算法在开始是用训练数据去初始化可见层,然后用条件分布计算隐层;然后,再根据隐层用条件分布来计算可见层。这样产生的结果是对输入的一个重构。CD算法将上述公式6表示为: