目录
先不管其他,拿一个例子来说明。

(1).输入的数据有15个
(2).建模。输出,中间层,输出层,每层应该选取多少个元素
(3).建立神经网络
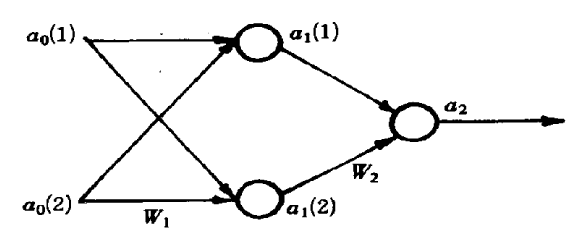
(4).规定目标为:当t(1)=0.9时表示是Apf类,当t(2)=0.1时表示是Af类
1 clc 2 clear all; 3 %输入数据 4 a0_ori=[ 1.78,1.96,1.86,1.72,2.00,2.00,1.96,1.74,1.64,1.82,1.90,1.70,1.82,1.82,2.08; 5 1.14,1.18,1.20,1.24,1.26,1.28,1.30,1.36,1.38,1.38,1.38,1.40,1.48,1.54,1.56]; 6 t=[0.9,0.9,0.9,0.1,0.9,0.9,0.9,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1]; 7 %数据拓展及信息提取 8 num_sample=length(a0_ori(1,:));%训练样本的数量 9 a0=[a0_ori;-ones(1,num_sample)];%加入常数项,固定为-1
给各连接权值一个(0,1)内的随机数,给定误差是E,给定计算精度是![]() 和最大学习次数M
和最大学习次数M

其中![]() 表示第i层第j个神经元的阈值。
表示第i层第j个神经元的阈值。
1 %初始化 2 t_max=5000;%最大迭代圈数 3 p_pre=0.01;%预设精度 4 e=0.1;%初始精度 5 w1=rand(2,3); 6 w2=rand(1,3); 7 eta=0.1;%收敛速度
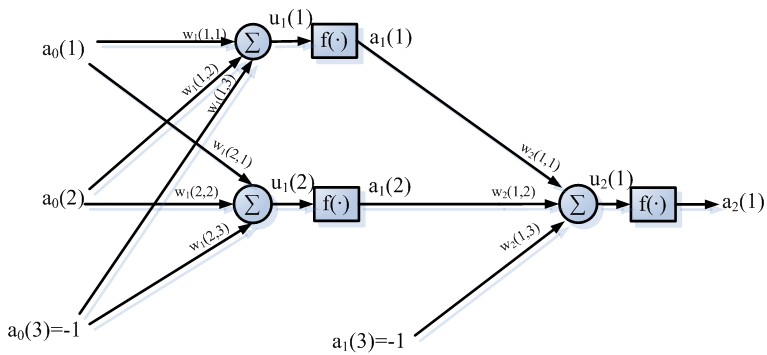
取![]() 将各神经元的阈值作为固定输入,则完善神经网络如下:
将各神经元的阈值作为固定输入,则完善神经网络如下:

则根据上图很容易知道网络隐含层输出:
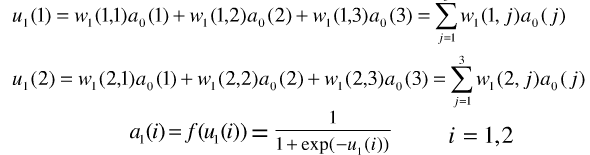
同理,输出神经元:
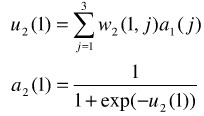
1 p=1;%迭代圈数初始化为1 2 while p<10000 & e>p_pre 3 for id_sample=1:num_sample %遍历样品 4 %3.根据输入数据计算网络输出 5 6 %计算第一层 7 u1(1)=w1(1,:)*a0(:,id_sample); 8 u1(2)=w1(2,:)*a0(:,id_sample); 9 a1(1:2,id_sample)=1./(1+exp(-u1(1:2))); 10 a1(3,id_sample)=-1; 11 12 %计算第二层 13 u2=w2(1,:)*a1(:,id_sample); 14 a2(id_sample)=1/(1+exp(-u2));
利用输出层各神经元的误差项![]() 和隐含层各神经元的输出来修正权值
和隐含层各神经元的输出来修正权值
取激励函数

![]() ,
,
则
![]() 。
。
可以据此计算输出层误差项
![]()
通过这个算法可以看出BP(Back Propagation)网络是一种按误差逆传播算法训练的多层前馈网络。在后向传播过程中,并非是进行逆运算,而是可以理解成直接把右图中的箭头反向进行运算。比如f(.)仍然是f(.),而不是变成f-1(.)
取学习速率![]() (或其他正数,可调整大小)
(或其他正数,可调整大小)
计算![]() ,
,![]()
![]()
1 %4.训练输出单元的权值 2 delta2=(t(id_sample)-a2(id_sample))*1/(1+exp(-u2))*(1-1/(1+exp(-u2))); 3 w2(1,:)=w2(1,:)+eta*delta2*a1(:,id_sample)';
利用隐含层各神经元的误差项和输入层各神经单元的输入来修正权值

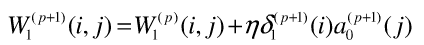
%5.训练隐藏单元的权值 delta1=a1(:,id_sample).*(1-a1(:,id_sample))*delta2.*w2(1,:)'; w1(1,:)=w1(1,:)+eta*delta1(1).*a0(:,id_sample)'; w1(2,:)=w1(2,:)+eta*delta1(2).*a0(:,id_sample)'; end
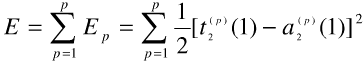
直到全局误差小于目标值或者到达预定迭代次数为止。
e=sum((t(:)-a2(:)).^2); p=p+1; end
1 clc 2 clear all; 3 %输入数据 4 a0_ori=[ 1.78,1.96,1.86,1.72,2.00,2.00,1.96,1.74,1.64,1.82,1.90,1.70,1.82,1.82,2.08; 5 1.14,1.18,1.20,1.24,1.26,1.28,1.30,1.36,1.38,1.38,1.38,1.40,1.48,1.54,1.56]; 6 t=[0.9,0.9,0.9,0.1,0.9,0.9,0.9,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1]; 7 %数据拓展及信息提取 8 num_sample=length(a0_ori(1,:));%训练样本的数量 9 a0=[a0_ori;-ones(1,num_sample)];%加入常数项,固定为-1 10 11 12 %初始化 13 t_max=5000;%最大迭代圈数 14 p_pre=0.01;%预设精度 15 e=0.1;%初始精度 16 w1=rand(2,3); 17 w2=rand(1,3); 18 eta=0.5;%收敛速度 19 20 p=1;%迭代圈数初始化为1 21 while p<t_max & e>p_pre 22 for id_sample=1:num_sample %遍历样品 23 %3.根据输入数据计算网络输出 24 25 %计算第一层 26 u1(1)=w1(1,:)*a0(:,id_sample); 27 u1(2)=w1(2,:)*a0(:,id_sample); 28 a1(1:2,id_sample)=1./(1+exp(-u1(1:2))); 29 a1(3,id_sample)=-1; 30 31 %计算第二层 32 u2=w2(1,:)*a1(:,id_sample); 33 a2(id_sample)=1/(1+exp(-u2)); 34 35 %4.训练输出单元的权值 36 delta2=(t(id_sample)-a2(id_sample))*1/(1+exp(-u2))*(1-1/(1+exp(-u2))); 37 w2(1,:)=w2(1,:)+eta*delta2*a1(:,id_sample)'; 38 39 %5.训练隐藏单元的权值 40 delta1=a1(:,id_sample).*(1-a1(:,id_sample))*delta2.*w2(1,:)'; 41 w1(1,:)=w1(1,:)+eta*delta1(1).*a0(:,id_sample)'; 42 w1(2,:)=w1(2,:)+eta*delta1(2).*a0(:,id_sample)'; 43 end 44 e=sum((t(:)-a2(:)).^2)/2; 45 p=p+1; 46 end
8.待解决问题
1.权值最终的结果是否是相对固定的?还是可能存在多解?是否有最优解?
2. 如果加入干扰项输入,其对应权值是否是接近0的值?
3.如果增加额外的神经元,神经网络的结构会产生和影响?
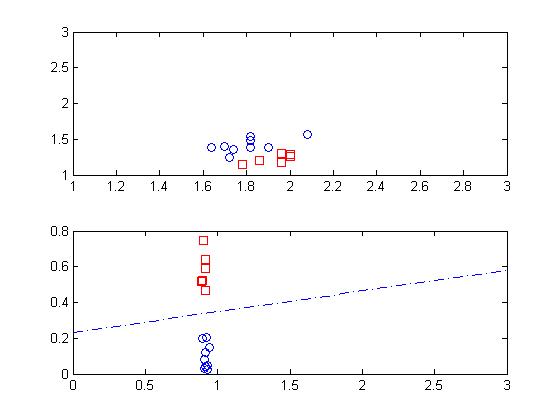
下图是样本的分布情况,从图中看出,该图是线性可分的。因此采用感知器完全可以解决这个问题。

1 clc 2 clear all; 3 %输入数据 4 a0_ori=[ 1.78,1.96,1.86,1.72,2.00,2.00,1.96,1.74,1.64,1.82,1.90,1.70,1.82,1.82,2.08; 5 1.14,1.18,1.20,1.24,1.26,1.28,1.30,1.36,1.38,1.38,1.38,1.40,1.48,1.54,1.56]; 6 t=[0.9,0.9,0.9,0.1,0.9,0.9,0.9,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1]; 7 a0_A=a0_ori(:,find(t==0.9)); 8 a0_B=a0_ori(:,find(t==0.1)); 9 plot(a0_A(1,:),a0_A(2,:),'rs'); 10 hold on; 11 plot(a0_B(1,:),a0_B(2,:),'o');

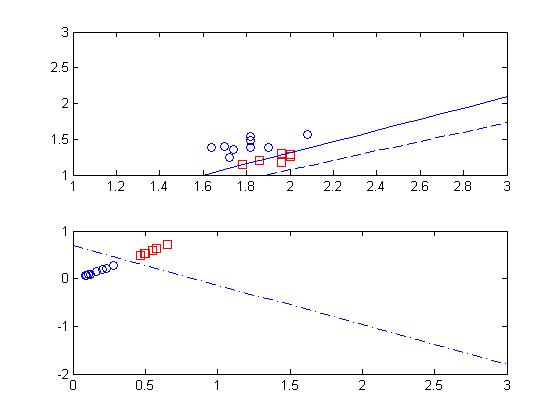
从下面的图可以看出,整个神经网络中,最终由效果的仅仅是输出层的神经元。

1 clc 2 clear all; 3 %输入数据 4 a0_ori=[ 1.78,1.96,1.86,1.72,2.00,2.00,1.96,1.74,1.64,1.82,1.90,1.70,1.82,1.82,2.08; 5 1.14,1.18,1.20,1.24,1.26,1.28,1.30,1.36,1.38,1.38,1.38,1.40,1.48,1.54,1.56]; 6 t=[0.9,0.9,0.9,0.1,0.9,0.9,0.9,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1]; 7 a0_A=a0_ori(:,find(t==0.9)); 8 a0_B=a0_ori(:,find(t==0.1)); 9 subplot(2,1,1); 10 plot(a0_A(1,:),a0_A(2,:),'rs'); 11 hold on; 12 plot(a0_B(1,:),a0_B(2,:),'o'); 13 hold on; 14 15 %数据拓展及信息提取 16 num_sample=length(a0_ori(1,:));%训练样本的数量 17 a0=[a0_ori;-ones(1,num_sample)];%加入常数项,固定为-1 18 19 20 %初始化 21 t_max=10000;%最大迭代圈数 22 p_pre=0.01;%预设精度 23 e=100;%初始精度 24 w1=rand(2,3)+0.5; 25 w2=rand(1,3)+0.5; 26 eta=0.1;%收敛速度 27 a=1; 28 29 p=1;%迭代圈数初始化为1 30 while p<t_max & e>p_pre 31 for id_sample=1:num_sample %遍历样品 32 %3.根据输入数据计算网络输出 33 34 %计算第一层 35 u1(1)=w1(1,:)*a0(:,id_sample); 36 u1(2)=w1(2,:)*a0(:,id_sample); 37 a1(1:2,id_sample)=1./(1+exp(-a*u1(1:2))); 38 a1(3,id_sample)=-1; 39 40 %计算第二层 41 u2=w2(1,:)*a1(:,id_sample); 42 a2(id_sample)=1/(1+exp(-u2)); 43 44 %4.训练输出单元的权值 45 delta2=(t(id_sample)-a2(id_sample))*1/(1+exp(-a*u2))*(1-1/(1+exp(-a*u2)))*a; 46 w2(1,:)=w2(1,:)+eta*delta2*a1(:,id_sample)'; 47 48 %5.训练隐藏单元的权值 49 delta1=a*a1(:,id_sample).*(1-a1(:,id_sample))*delta2.*w2(1,:)'; 50 w1(1,:)=w1(1,:)+eta*delta1(1).*a0(:,id_sample)'; 51 w1(2,:)=w1(2,:)+eta*delta1(2).*a0(:,id_sample)'; 52 end 53 e=sum((t(:)-a2(:)).^2)/2; 54 p=p+1; 55 end 56 57 x=0:0.1:3; 58 y=(w1(1,3)-w1(1,1).*x)/w1(1,2); 59 plot(x,y,'-');hold on 60 y=(w1(2,3)-w1(1,1).*x)/w1(2,2); 61 plot(x,y,'--');axis([1,3,1,3]) 62 63 subplot(2,1,2); 64 a1_A=a1(:,find(t==0.9)); 65 a1_B=a1(:,find(t==0.1)); 66 plot(a1_A(1,:),a1_A(2,:),'rs'); 67 hold on; 68 plot(a1_B(1,:),a1_B(2,:),'o'); 69 hold on; 70 y=(w2(1,3)-w2(1,1).*x)/w2(1,2); 71 plot(x,y,'-.');
9.权值初始值的研究
权值初始值是否对后面的结果有影响呢,如果是异或分布的样本,通过BP方法是否能让第一层权值对应的直线十字叉分布呢

1 clc 2 clear all; 3 %输入数据 4 a0_ori=[ 0.5,0.96,0.86,0.72,2.00,2.00,1.06,1.54,1.24,1.82,1.90,1.70,0.82,0.82,0.08,0.54; 5 1.14,1.18,1.20,1.24,0.26,0.28,0.30,0.36,1.38,1.38,1.38,1.40,0.48,0.54,0.56,0.35]; 6 7 t=[0.9,0.9,0.9,0.9,0.9,0.9,0.9,0.9,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1]; 8 a0_A=a0_ori(:,find(t==0.9)); 9 a0_B=a0_ori(:,find(t==0.1)); 10 % subplot(2,1,1); 11 12 13 %数据拓展及信息提取 14 num_sample=length(a0_ori(1,:));%训练样本的数量 15 a0=[a0_ori;-ones(1,num_sample)];%加入常数项,固定为-1 16 17 18 %初始化 19 t_max=100000;%最大迭代圈数 20 p_pre=0.01;%预设精度 21 e=100;%初始精度 22 % w1=rand(2,3)+0.5; 23 % w2=rand(1,3)+0.5; 24 w1=[2,1,1;1,2,1]; 25 w2=[1,2,1]; 26 eta=0.5;%收敛速度 27 a=1; 28 29 p=1;%迭代圈数初始化为1 30 while p<t_max & e>p_pre 31 32 for id_sample=1:num_sample %遍历样品 33 %3.根据输入数据计算网络输出 34 35 %计算第一层 36 u1(1)=w1(1,:)*a0(:,id_sample); 37 u1(2)=w1(2,:)*a0(:,id_sample); 38 a1(1:2,id_sample)=1./(1+exp(-a*u1(1:2))); 39 a1(3,id_sample)=-1; 40 41 %计算第二层 42 u2=w2(1,:)*a1(:,id_sample); 43 a2(id_sample)=1/(1+exp(-a*u2)); 44 45 %4.训练输出单元的权值 46 delta2=(t(id_sample)-a2(id_sample))*a2(id_sample)*(1-a2(id_sample))*a; 47 w2(1,:)=w2(1,:)+eta*delta2*a1(:,id_sample)'; 48 49 %5.训练隐藏单元的权值 50 delta1=a*a1(:,id_sample).*(1-a1(:,id_sample))*delta2.*w2(1,:)'; 51 w1(1,:)=w1(1,:)+eta*delta1(1).*a0(:,id_sample)'; 52 w1(2,:)=w1(2,:)+eta*delta1(2).*a0(:,id_sample)'; 53 end 54 e=sum((t(:)-a2(:)).^2)/2; 55 p=p+1; 56 57 if mod(p,500)==0 58 subplot(2,1,1); 59 plot(a0_A(1,:),a0_A(2,:),'rs'); 60 hold on; 61 plot(a0_B(1,:),a0_B(2,:),'o'); 62 hold on; 63 x=0:0.1:2; 64 y=(w1(1,3)-w1(1,1).*x)/w1(1,2); 65 plot(x,y,'--'); 66 hold on 67 y=(w1(2,3)-w1(2,1).*x)/w1(2,2); 68 plot(x,y,'-.');axis([0,2,0,2]) 69 hold off 70 subplot(2,1,2); 71 a1_A=a1(:,find(t==0.9)); 72 a1_B=a1(:,find(t==0.1)); 73 plot(a1_A(1,:),a1_A(2,:),'rs'); 74 hold on; 75 plot(a1_B(1,:),a1_B(2,:),'o'); 76 hold on; 77 y=(w2(1,3)-w2(1,1).*x)/w2(1,2); 78 plot(x,y,'-');axis([0,2,0,2]) 79 hold off 80 end 81 end
9.1两个初始权值对应直线均为负斜率
w1=[2,1,1;1,2,1];
w2=[1,2,1];
下面的图中前三个间隔均为500轮循环,经过约3000轮到达第四幅图的结果。
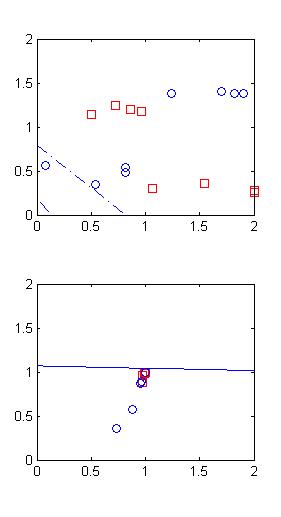


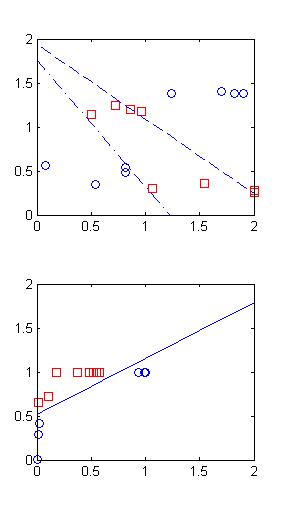
如果把初值设为
w1=[2,-3,1;1,-6,1];
w2=[1,5,1];
最后结果为:
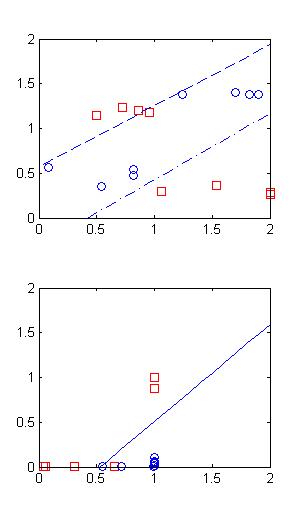
如果把初值设为
w1=[0.01,1,1;1,-0.01,1];
w2=[1,5,1];即如左图所示,则最后得到右图的结果.
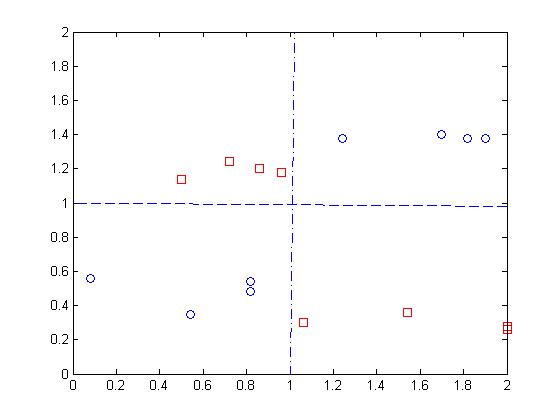
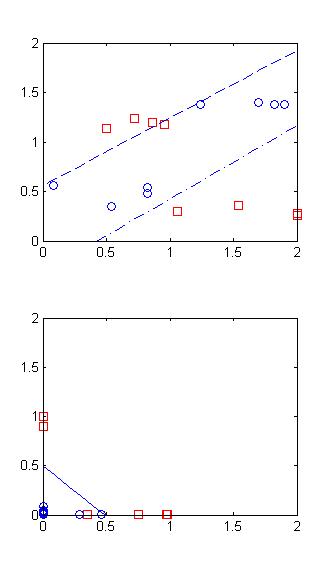
但从左图可以看出,初始值已经完美的区分了两个类别,经过优化之后,区分能力反而有所降低。这是由于神经网络对于异或问题的解决 限制 决定的 。
10.拓展的异或问题
对于上面的样本分布基本还是异或问题的拓展,我们称之为拓展的异或问题。当分布进一步分散(如下图所示)时,很难在第一步用两条直线进行区分。

对于这类问题,一个可行的方法是通过增加一个额外的节点来解决
