《基于Python的GMSSL实现》课程设计个人报告
一、基本信息
题目:GMSSL基于python的实现
指导老师:LJP
完成时间:2019年5月6日---2019年5月26日
验收时间:2019年5月27日
小组成员:YJT,TX,LJF
二、个人贡献
1. 收集相关资料并分享(相关博客、Python教程等)
2. 学习并搭建实验所需环境
3. 实现sm4算法的加解密
三、任务内容
1. 用Python语句调用gmssl以实现sm4
2. 实现用gmssl加密通信的功能
四、实践过程
(一)学习并熟悉Python
思维导图如下:

(二)上手SM4算法
国产密码算法介绍
国产密码算法(国密算法)是指国家密码局认定的国产商用密码算法,在金融领域目前主要使用公开的SM2、SM3、SM4三类算法,分别是非对称算法、哈希算法和对称算法。
SM2算法:SM2椭圆曲线公钥密码算法是我国自主设计的公钥密码算法,包括SM2-1椭圆曲线数字签名算法,SM2-2椭圆曲线密钥交换协议,SM2-3椭圆曲线公钥加密算法,分别用于实现数字签名密钥协商和数据加密等功能。SM2算法与RSA算法不同的是,SM2算法是基于椭圆曲线上点群离散对数难题,相对于RSA算法,256位的SM2密码强度已经比2048位的RSA密码强度要高。
SM3算法:SM3杂凑算法是我国自主设计的密码杂凑算法,适用于商用密码应用中的数字签名和验证消息认证码的生成与验证以及随机数的生成,可满足多种密码应用的安全需求。为了保证杂凑算法的安全性,其产生的杂凑值的长度不应太短,例如MD5输出128比特杂凑值,输出长度太短,影响其安全性SHA-1算法的输出长度为160比特,SM3算法的输出长度为256比特,因此SM3算法的安全性要高于MD5算法和SHA-1算法。
SM4算法:SM4分组密码算法是我国自主设计的分组对称密码算法,用于实现数据的加密/解密运算,以保证数据和信息的机密性。要保证一个对称密码算法的安全性的基本条件是其具备足够的密钥长度,SM4算法与AES算法具有相同的密钥长度分组长度128比特,因此在安全性上高于3DES算法。
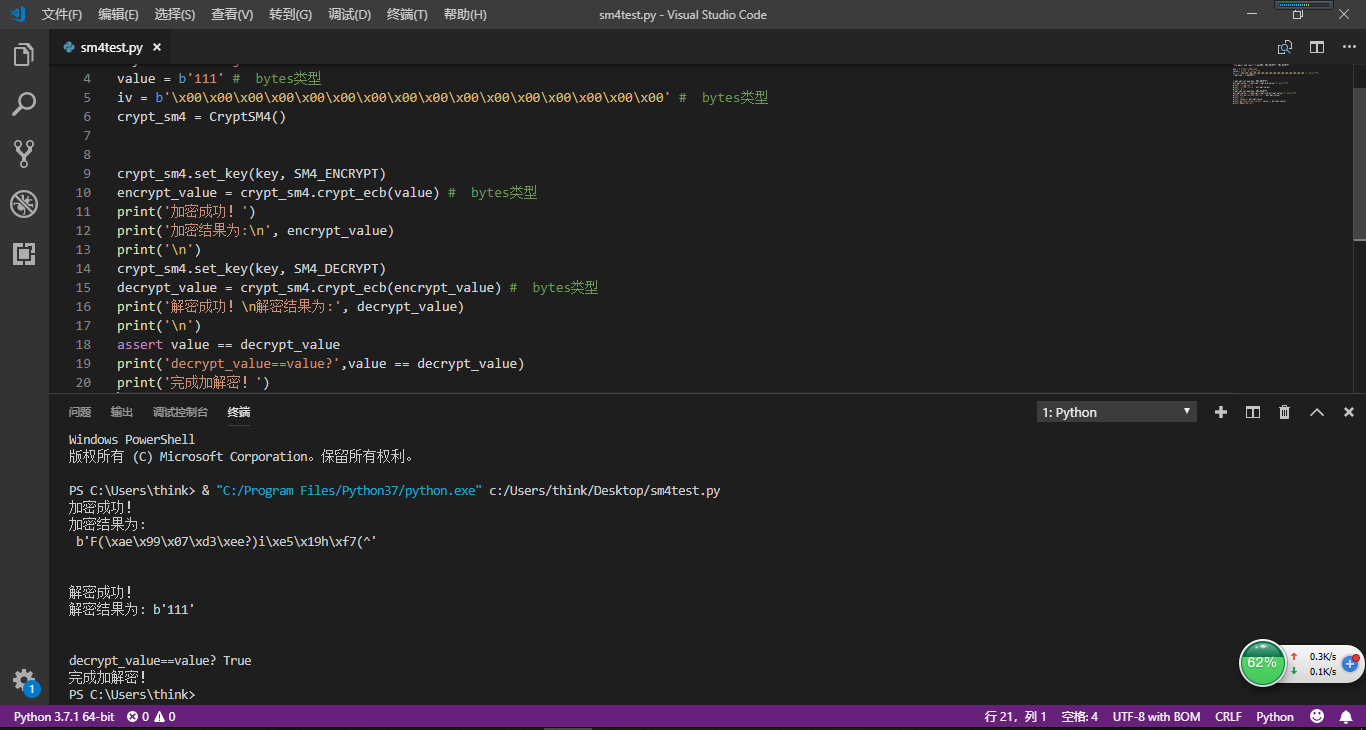
完成SM4算法的代码
from gmssl.sm4 import CryptSM4, SM4_ENCRYPT, SM4_DECRYPT key = b'3l5butlj26hvv313' value = b'111' # bytes类型 iv = b'x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00x00' # bytes类型 crypt_sm4 = CryptSM4() crypt_sm4.set_key(key, SM4_ENCRYPT) encrypt_value = crypt_sm4.crypt_ecb(value) # bytes类型 print('加密成功!') print('加密结果为: ', encrypt_value) print(' ') crypt_sm4.set_key(key, SM4_DECRYPT) decrypt_value = crypt_sm4.crypt_ecb(encrypt_value) # bytes类型 print('解密成功! 解密结果为:', decrypt_value) print(' ') assert value == decrypt_value print('decrypt_value==value?',value == decrypt_value) print('完成加解密!')
五、实验中遇到的问题
在安装gmssl时遇到了如下问题:
由红色报错内容可猜测是权限问题
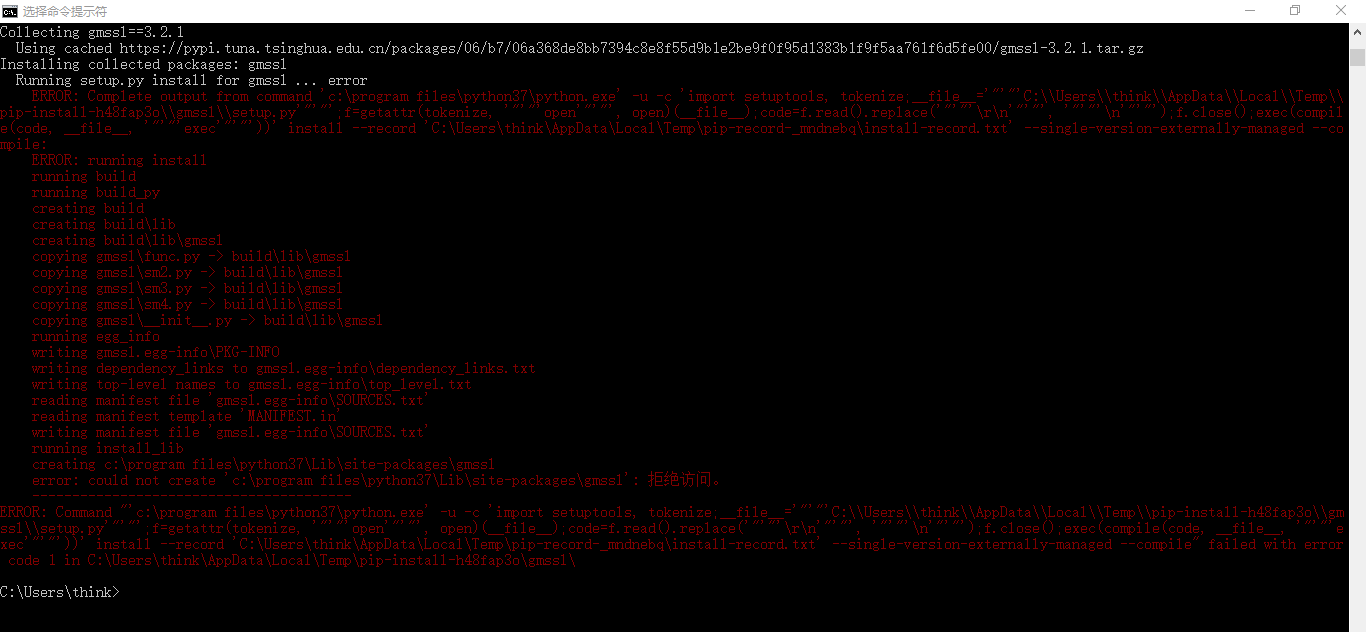
更换至管理员权限的命令行,成功解决:
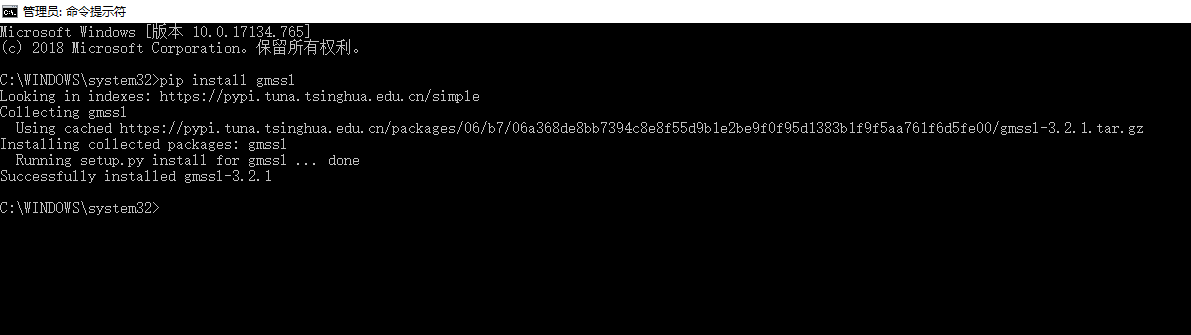
六、设计体会及收获
我负责的部分是实现sm4算法,中途和老师交流以后发现我们小组对题目理解有偏差,应该做的是用Python语句调用gmssl以实现相应的功能。
从前两周的探索到最终成功,从学习基本语言到深入理解算法再到最终实现自己负责的板块,收获很大,同时也要感谢老师和队友整个过程的帮助!