目录
定义
1 常规方法判断
2 最有效方法判断
3 测试
定义
约数只有1和本身的整数称为质数,或称素数。
1 常规方法判断
根据定义,因为质数除了1和本身之外没有其他约数,所以判断n是否为质数,根据定义直接判断从2到n-1是否存在n的约数即可。
Java代码如下:
1 /** 2 * 判断是否为素数/质数的常规方法 3 * 判断n是否为素数,根据定义直接判断从2到n-1是否存在n的约数即可 4 * @param num 5 * @return 6 */ 7 public static boolean isPrimeNormal(int num) { 8 for(int i=2; i<num; i++) { 9 if(num%i == 0) { 10 return false; 11 } 12 } 13 14 return true; 15 } 16
2 最有效方法判断
首先看一个关于质数分布的规律:大于等于5的质数一定和6的倍数相邻,例如5和7,11和13,17和19等等。
证明:令x≥1,将大于等于5的自然数表示如下:
······ 6x-1,6x,6x+1,6x+2,6x+3,6x+4,6x+5,6(x+1),6(x+1)+1 ······
可以看到,不在6的倍数两侧,即6x两侧的数为6x+2,6x+3,6x+4,由于2(3x+1),3(2x+1),2(3x+2),所以它们一定不是素数,再除去6x本身,显然,素数要出现只可能出现在6x的相邻两侧。
另外,我们知道,一个数若可以进行因数分解,那么分解时得到的两个数一定是一个小于等于sqrt(n),一个大于等于sqrt(n),据此,上述代码中并不需要遍历到n-1,遍历到sqrt(n)即可,因为若sqrt(n)左侧找不到约数,那么右侧也一定找不到约数。
Java代码如下:
1 /** 2 * 判断是否为素数/质数的最有效方法 3 * 1.小于5的2和3 4 * 2.大于等于5的素数一定和6的倍数相邻,例如5和7,11和13,17和19等等。 5 * @param num 6 * @return 7 */ 8 public static boolean isPrime(int num) { 9 //两个较小数另外处理 10 if(num==2 || num==3) { 11 return true; 12 } 13 14 //不在6的倍数两侧的一定不是素数 15 if(num%6!=1 && num%6!=5) { 16 return false; 17 } 18 19 int tmp = (int) Math.sqrt(num);//获取平方根 20 //在6的倍数两侧的也可能不是素数 21 for(int i=5; i<=tmp; i+=6) { 22 if(num%i==0 || num%(i+2)==0) { 23 return false; 24 } 25 } 26 27 return true; 28 }
下面来看下,这两个方法的性能测试:
1 public static void main(String[] args) { 2 int testNum = 1000000; 3 4 //常规方法测试 5 long start1 = Calendar.getInstance().getTimeInMillis(); 6 for(int i=0; i<testNum; i++) { 7 isPrimeNormal(i); 8 } 9 long end1 = Calendar.getInstance().getTimeInMillis(); 10 System.out.println("常规方法,消耗时长(ms):" + (end1 - start1)); 11 12 //最有效方法测试 13 long start2 = Calendar.getInstance().getTimeInMillis(); 14 for(int i=0; i<testNum; i++) { 15 isPrime(i); 16 } 17 long end2 = Calendar.getInstance().getTimeInMillis(); 18 System.out.println("最有效方法,消耗时长(ms):" + (end2 - start2)); 19 }
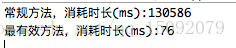
3 测试
测试结果如下:
最后,注明下此算法思想出自:https://blog.csdn.net/huang_miao_xin/article/details/51331710
https://blog.csdn.net/qq_15092079/article/details/80804326