题目描述
如题,给出一个网络图,以及其源点和汇点,求出其网络最大流。
输入输出格式
输入格式:
第一行包含四个正整数N、M、S、T,分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来M行每行包含三个正整数ui、vi、wi,表示第i条有向边从ui出发,到达vi,边权为wi(即该边最大流量为wi)
输出格式:
一行,包含一个正整数,即为该网络的最大流。
输入输出样例
输入样例#1:
4 5 4 3 4 2 30 4 3 20 2 3 20 2 1 30 1 3 40
输出样例#1:
50
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=10,M<=25
对于70%的数据:N<=200,M<=1000
对于100%的数据:N<=10000,M<=100000
样例说明:
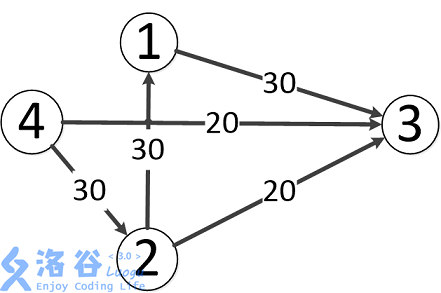
题目中存在3条路径:
4-->2-->3,该路线可通过20的流量
4-->3,可通过20的流量
4-->2-->1-->3,可通过10的流量(边4-->2之前已经耗费了20的流量)
故流量总计20+20+10=50。输出50。
思路:
裸最大流;
来,上代码:
#include <cstdio> #include <iostream> #define LL long long #define maxn 10005 #define maxm 100005 using namespace std; struct EdgeType { LL v,e,f; }; struct EdgeType edge[maxn<<5]; LL if_z,n,m,s,t,cnt=1,head[maxn],deep[maxn]; LL que[maxn<<9],h,tail,ans; char Cget; inline void in(LL &now) { now=0,if_z,Cget=getchar(); while(Cget>'9'||Cget<'0') { if(Cget=='-') if_z=-1; Cget=getchar(); } while(Cget>='0'&&Cget<='9') { now=now*10+Cget-'0'; Cget=getchar(); } } bool BFS() { for(LL i=1;i<=n;i++) deep[i]=-1; h=0,tail=1,deep[s]=0,que[h]=s; while(h<tail) { for(LL i=head[que[h]];i;i=edge[i].e) if(deep[edge[i].v]<0&&edge[i].f) { deep[edge[i].v]=deep[que[h]]+1; if(edge[i].v==t) return true; que[tail++]=edge[i].v; } h++; } return false; } LL flowing(LL now,LL flow) { if(now==t||!flow) return flow; LL oldflow=0; for(LL i=head[now];i;i=edge[i].e) { if(edge[i].f<=0||deep[edge[i].v]!=deep[now]+1) continue; LL pos=flowing(edge[i].v,min(flow,edge[i].f)); flow-=pos; oldflow+=pos; edge[i].f-=pos; edge[i^1].f+=pos; if(flow==0) return oldflow; } if(oldflow==0) deep[now]=-1; return oldflow; } int main() { in(n),in(m),in(s),in(t); LL u,v,w; while(m--) { in(u),in(v),in(w); edge[++cnt].v=v,edge[cnt].f=w,edge[cnt].e=head[u],head[u]=cnt; edge[++cnt].v=u,edge[cnt].f=0,edge[cnt].e=head[v],head[v]=cnt; } while(BFS()) ans+=flowing(s,0x7fffffff); cout<<ans; return 0; }