本文主要将逻辑回归的实现,模型的检验等
参考博文http://blog.csdn.net/tiaaaaa/article/details/58116346;http://blog.csdn.net/ai_vivi/article/details/43836641
1.测试集和训练集(3:7比例)数据来源:http://archive.ics.uci.edu/ml/datasets/statlog+(australian+credit+approval)
austra=read.table("australian.dat")
head(austra) #预览前6行
N=length(austra$V15) #690行,15列
#ind=1,ind=2分别以0.7,0.3的概率出现
ind=sample(2,N,replace=TRUE,prob=c(0.7,0.3))
aus_train=austra[ind==1,]
aus_test=austra[ind==2,]
2. 逻辑回归的实现及预测
pre=glm(V15~.,data=aus_train,family=binomial(link="logit")) summary(pre) real=aus_test$V15 predict_=predict.glm(pre,type="response",newdata=aus_test) predict=ifelse(predict_>0.5,1,0) aus_test$predict=predict head(aus_test) #write.csv(aus_test,"aus_test.csv")
3.模型检验
res=data.frame(real,predict) n=nrow(aus_train)
#计算Cox-Snell拟合优度 R2=1-exp((pre$deviance-pre$null.deviance)/n) cat("Cox-Snell R2=",R2," ") #Cox-Snell R2= 0.5502854
#计算Nagelkerke拟合优度 R2=R2/(1-exp((-pre$null.deviance)/n)) cat("Nagelkerke R2=",R2," ") #Nagelkerke R2= 0.7379711 #模型其他指标 #residuals(pre) #残差 #coefficients(pre) #系数 #anova(pre) #方差
4.准确率和精度
true_value=aus_test[,15] predict_value=aus_test[,16] #计算模型精度 error=predict_value-true_value #判断正确的数量占总数的比例 accuracy=(nrow(aus_test)-sum(abs(error)))/nrow(aus_test) #混淆矩阵中的量(混淆矩阵具体解释见下页) #真实值预测值全为1 / 预测值全为1 --- 提取出的正确信息条数/提取出的信息条数 precision=sum(true_value & predict_value)/sum(predict_value) #真实值预测值全为1 / 真实值全为1 --- 提取出的正确信息条数 /样本中的信息条数 recall=sum(predict_value & true_value)/sum(true_value) #P和R指标有时候会出现的矛盾的情况,这样就需要综合考虑他们,最常见的方法就是F-Measure(又称为F-Score) F_measure=2*precision*recall/(precision+recall) #F-Measure是Precision和Recall加权调和平均,是一个综合评价指标 #输出以上各结果 print(accuracy) print(precision) print(recall) print(F_measure) #混淆矩阵,显示结果依次为TP、FN、FP、TN table(true_value,predict_value)
5. ROC曲线
#ROC曲线 (ROC曲线详细解释见下页)
# 方法1
#install.packages("ROCR")
library(ROCR)
pred <- prediction(predict_,true_value) #预测值(0.5二分类之前的预测值)和真实值
performance(pred,'auc')@y.values #AUC值 0.9191563
perf <- performance(pred,'tpr','fpr') #y轴为tpr(true positive rate),x轴为fpr(false positive rate)
plot(perf)
#方法2
#install.packages("pROC")
library(pROC)
modelroc <- roc(true_value,predict.)
plot(modelroc, print.auc=TRUE, auc.polygon=TRUE,legacy.axes=TRUE, grid=c(0.1, 0.2),
grid.col=c("green", "red"), max.auc.polygon=TRUE,
auc.polygon.col="skyblue", print.thres=TRUE) #画出ROC曲线,标出坐标,并标出AUC的值
#方法3,按ROC定义
TPR=rep(0,1000)
FPR=rep(0,1000)
p=predict.
for(i in 1:1000)
{
p0=i/1000;
ypred<-1*(p>p0)
TPR[i]=sum(ypred*true_value)/sum(true_value)
FPR[i]=sum(ypred*(1-true_value))/sum(1-true_value)
}
plot(FPR,TPR,type="l",col=2)
points(c(0,1),c(0,1),type="l",lty=2)
6. 更换测试集和训练集的选取方式,采用十折交叉验证
australian <- read.table("australian.dat")
#将australian数据分成随机十等分
#install.packages("caret")
#固定folds函数的分组
set.seed(7)
library(caret)
folds <- createFolds(y=australian$V15,k=10)
#构建for循环,得10次交叉验证的测试集精确度、训练集精确度
max=0
num=0
for(i in 1:10){
fold_test <- australian[folds[[i]],] #取folds[[i]]作为测试集
fold_train <- australian[-folds[[i]],] # 剩下的数据作为训练集
print("***组号***")
fold_pre <- glm(V15 ~.,family=binomial(link='logit'),data=fold_train)
fold_predict <- predict(fold_pre,type='response',newdata=fold_test)
fold_predict =ifelse(fold_predict>0.5,1,0)
fold_test$predict = fold_predict
fold_error = fold_test[,16]-fold_test[,15]
fold_accuracy = (nrow(fold_test)-sum(abs(fold_error)))/nrow(fold_test)
print(i)
print("***测试集精确度***")
print(fold_accuracy)
print("***训练集精确度***")
fold_predict2 <- predict(fold_pre,type='response',newdata=fold_train)
fold_predict2 =ifelse(fold_predict2>0.5,1,0)
fold_train$predict = fold_predict2
fold_error2 = fold_train[,16]-fold_train[,15]
fold_accuracy2 = (nrow(fold_train)-sum(abs(fold_error2)))/nrow(fold_train)
print(fold_accuracy2)
if(fold_accuracy>max)
{
max=fold_accuracy
num=i
}
}
print(max)
print(num)
##结果可以看到,精确度accuracy最大的一次为max,取folds[[num]]作为测试集,其余作为训练集。
7.十折交叉验证的准确度
#十折里测试集最大精确度的结果 testi <- australian[folds[[num]],] traini <- australian[-folds[[num]],] # 剩下的folds作为训练集 prei <- glm(V15 ~.,family=binomial(link='logit'),data=traini) predicti <- predict.glm(prei,type='response',newdata=testi) predicti =ifelse(predicti>0.5,1,0) testi$predict = predicti #write.csv(testi,"ausfold_test.csv") errori = testi[,16]-testi[,15] accuracyi = (nrow(testi)-sum(abs(errori)))/nrow(testi) #十折里训练集的精确度 predicti2 <- predict.glm(prei,type='response',newdata=traini) predicti2 =ifelse(predicti2>0.5,1,0) traini$predict = predicti2 errori2 = traini[,16]-traini[,15] accuracyi2 = (nrow(traini)-sum(abs(errori2)))/nrow(traini) #测试集精确度、取第i组、训练集精确 accuracyi;num;accuracyi2 #write.csv(traini,"ausfold_train.csv")
混淆矩阵
| 预测 | ||||
| 1 | 0 | |||
| 实 | 1 | True Positive(TP) | True Negative(TN) | Actual Positive(TP+TN) |
| 际 | 0 | False Positive(FP) | False Negative(FN) | Actual Negative(FP+FN) |
| Predicted Positive(TP+FP) | Predicted Negative(TN+FN) | (TP+TN+FP+FN) |
AccuracyRate(准确率): (TP+TN)/(TP+TN+FN+FP)
ErrorRate(误分率): (FN+FP)/(TP+TN+FN+FP)
Recall(召回率,查全率,击中概率): TP/(TP+FN), 在所有GroundTruth为正样本中有多少被识别为正样本了;
Precision(查准率):TP/(TP+FP),在所有识别成正样本中有多少是真正的正样本;
TPR(True Positive Rate): TP/(TP+FN),实际就是Recall
FAR(False Acceptance Rate)或FPR(False Positive Rate):FP/(FP+TN), 错误接收率,误报率,在所有GroundTruth为负样本中有多少被识别为正样本了;
FRR(False Rejection Rate): FN/(TP+FN),错误拒绝率,拒真率,在所有GroundTruth为正样本中有多少被识别为负样本了,它等于1-Recall
ROC曲线(receiver operating characteristic curve)
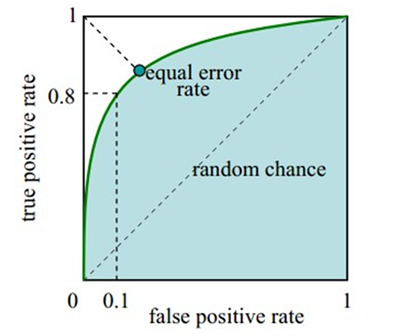
-
横轴是FPR,纵轴是TPR;
-
每个阈值的识别结果对应一个点(FPR,TPR),当阈值最大时,所有样本都被识别成负样本,对应于左下角的点(0,0),当阈值最小时,所有样本都被识别成正样本,对应于右上角的点(1,1),随着阈值从最大变化到最小,TP和FP都逐渐增大;
-
一个好的分类模型应尽可能位于图像的左上角,而一个随机猜测模型应位于连接点(TPR=0,FPR=0)和(TPR=1,FPR=1)的主对角线上;
-
可以使用ROC曲线下方的面积AUC(AreaUnder roc Curve)值来度量算法好坏:如果模型是完美的,那么它的AUG = 1,如果模型是个简单的随机猜测模型,那么它的AUG = 0.5,如果一个模型好于另一个,则它的曲线下方面积相对较大;
-
ERR(Equal Error Rate,相等错误率):FAR和FRR是同一个算法系统的两个参数,把它放在同一个坐标中。FAR是随阈值增大而减小的,FRR是随阈值增大而增大的。因此它们一定有交点。这个点是在某个阈值下的FAR与FRR等值的点。习惯上用这一点的值来衡量算法的综合性能。对于一个更优的指纹算法,希望在相同阈值情况下,FAR和FRR都越小越好。