题目描述
给定一个数组A[0,1,...,n-1],请构建一个数组B[0,1,...,n-1],其中B中的元素B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]。不能使用除法。(注意:规定B[0] = A[1] * A[2] * ... * A[n-1],B[n-1] = A[0] * A[1] * ... * A[n-2];)
对于A长度为1的情况,B无意义,故而无法构建,因此该情况不会存在。
思路
不能用除法,正常连乘的话时间复杂度为0(n^2)
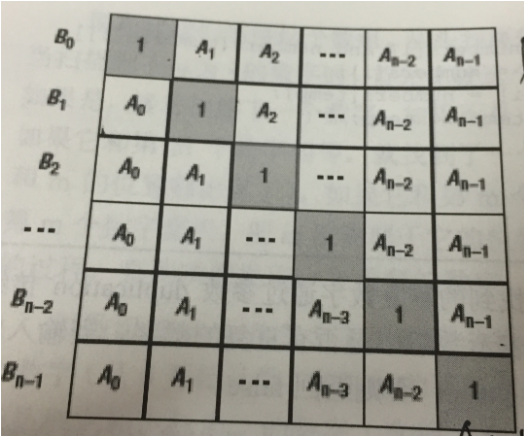
可以发现:
B[i]的左下三角和B[i-1]有关(将B[i]的左半部分乘积看成C[i],有C[i]=C[i-1]*A[i-1])
B[i]的右上三角与B[i+1]有关(将B[i]的右半部分乘积看成D[i],有D[i]=D[i+1]*A[i+1])
因此,可以先算 下三角 中的连乘,这样求得B[i] 的一部分,然后倒过来利用 上三角 计算B[i] 另一部分。
解法
public class Solution { public int[] multiply(int[] A) { int[] B = new int[A.length]; if (A.length == 0) return B; B[0] = 1; // 先计算下三角 for (int i = 1; i < A.length; i++) { B[i] = B[i-1] * A[i - 1]; } // 计算上三角 int temp = 1; for (int j = A.length - 2; j >= 0; j--) { temp *= A[j + 1]; B[j] *= temp; } return B; } }