形式:求n个点____ 的个数
有标号无向图的个数(不一定联通):(2^{C_n^2})
证明显然
有标号无向联通图个数:
设g(x)为不一定联通图的个数, f(x) 为连通图个数
枚举1号点所在联通块的大小
(g(x) = displaystyle sum_{i=1}^{n}{n - 1 choose i - 1}f(i) * g(n - i))
最后将(g(x) = 2^{C_n^2})带进去即可
(多项式我不会。。。)
所有点度数都是偶数的有标号图(不一定联通) : (2^{C_{n-1}^2})
可以将1-n-1的点任意连起来
可以证明一个图中度数为奇数的点有偶数个
那么将点n将1-n-1度数为奇的点连起来
所有的点度数都将成为偶数
所有点度数都是偶数的有标号图(联通) :
类似的
设g(x)为不一定联通图的个数, f(x) 为连通图个数
枚举1号点所在联通块的大小
(g(x) = displaystyle sum_{i=1}^{n}{n - 1 choose i - 1}f(i) * g(n - i))
(f(x) = g(x) - displaystyle sum_{i=1}^{n-1}{n - 1 choose i - 1}f(i) * g(n - i))
无标号有根树:$ n ^ {n-2}$
也可以说n个点完全图生成树的个数
引理: prufer序列
prufer是一种无根树的编码表示, 对于一棵n节点无根树,唯一对应一个长度为n-2的序列
理解:prufer将树的n-2个父亲节点(可重复)加上神奇的构造方式表示每个父亲的儿子, 即表示了每条边;
(1) 无根树转prufer序列
操作:每次取叶子节点(度数为1)中标号最小的一个,将它的父亲节点加入序列, 并将其删除
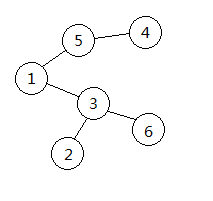
如图的序列为: 3 5 1 3
用set实现
有一个性质: 某个编号出现的次数等于这个节点在无根树中的度数
(2)prufer序列转无根树
设节点集合v={1,2,3...n}, prufer序列集合A={(a_1,a_2...,a_{n-2})}
每次取出prufer序列最前面的编号u, 找到v中最小的且未在A中的点v,
将u,v连边, 在两个集合中分别删去它们;
依然用set搞定
由此说明任意一个n-2序列都可得到一棵不同的无根树
无根树的个数为:$ n ^ {n-2}$
一个有趣的推广是,n个节点的度依次为D1, D2, …, Dn的无根树共有(n-2)! / [ (D1-1)!(D2-1)!..(Dn-1)! ]个,因为此时Prüfer编码中的数字i恰好出现Di-1次。
有标号有根树: $ n ^ {n-1}$
即每棵无根树的每个节点都可以当根, 再乘上n即可