该系列为DR_CAN Advanced控制理论视频笔记,详见https://space.bilibili.com/230105574
由于笔者水平有限,文中难免存在一些不足和错误之处,诚请各位批评指正。
1 弹簧阻尼系统的例子
根据牛顿第二定理我们可以得到弹簧阻尼系统的微分方程:
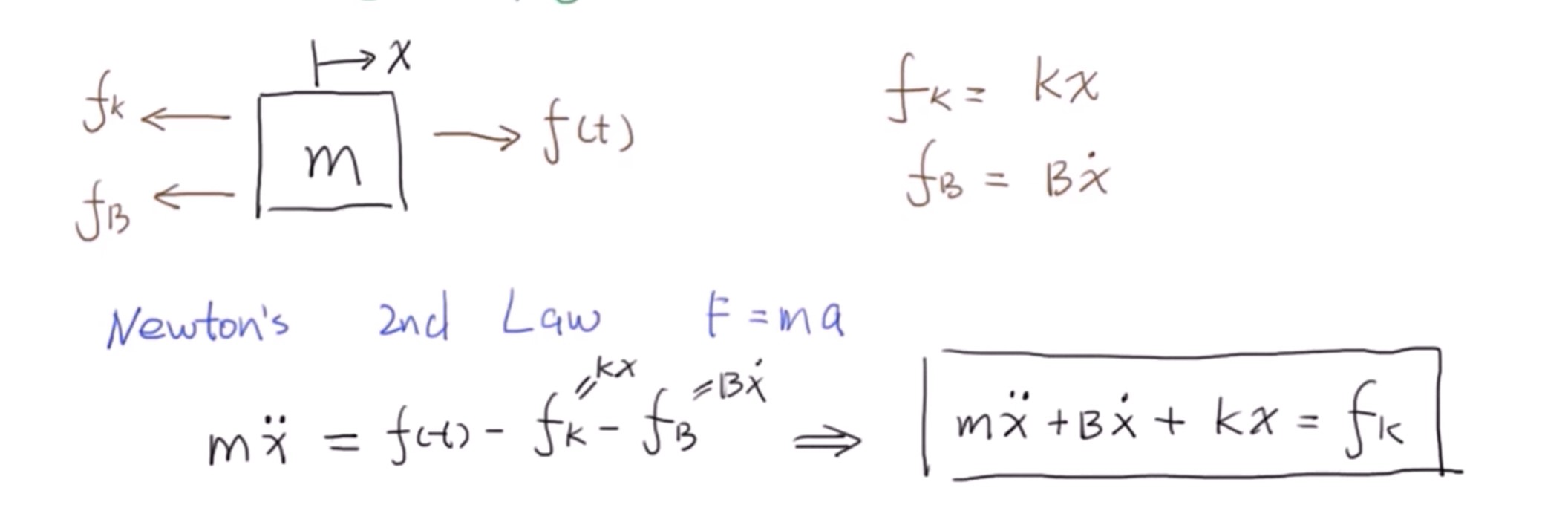
在现代控制理论中,我们通过状态空间来描述这个系统,状态空间可以理解为一个包含输入、输出、状态变量的集合,并用一个一阶微分方程的形式表示出来:


2 状态空间方程与传递函数
我们对系统状态空间方程和输出分别进行拉普拉斯变换,经过代入计算我们可以得到与直接对微分方程进行拉普拉斯变换相同的传递函数:


我们发现,传递函数的分母部分和行列式 (|sI-A|) 息息相关的,而当 (|sI-A|=0) 时,(s) 便是 (A) 矩阵的特征值。而对于传递函数来讲,分母为零时 (s) 便是系统的极点。而在经典控制理论中系统的极点决定着系统的稳定性,而 (A) 矩阵的特征值同样决定着系统的稳定性。实际上这两者是相等的。
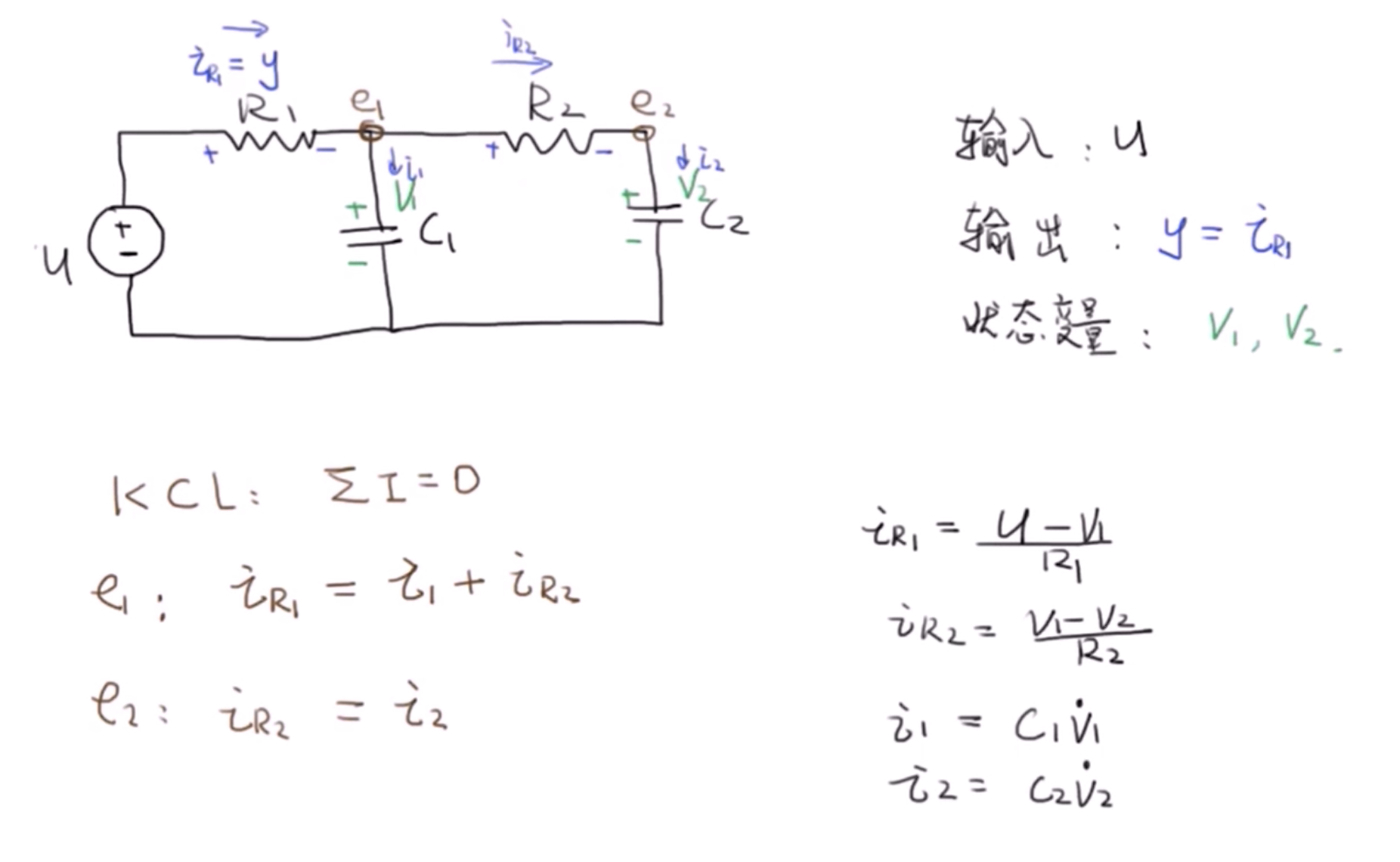
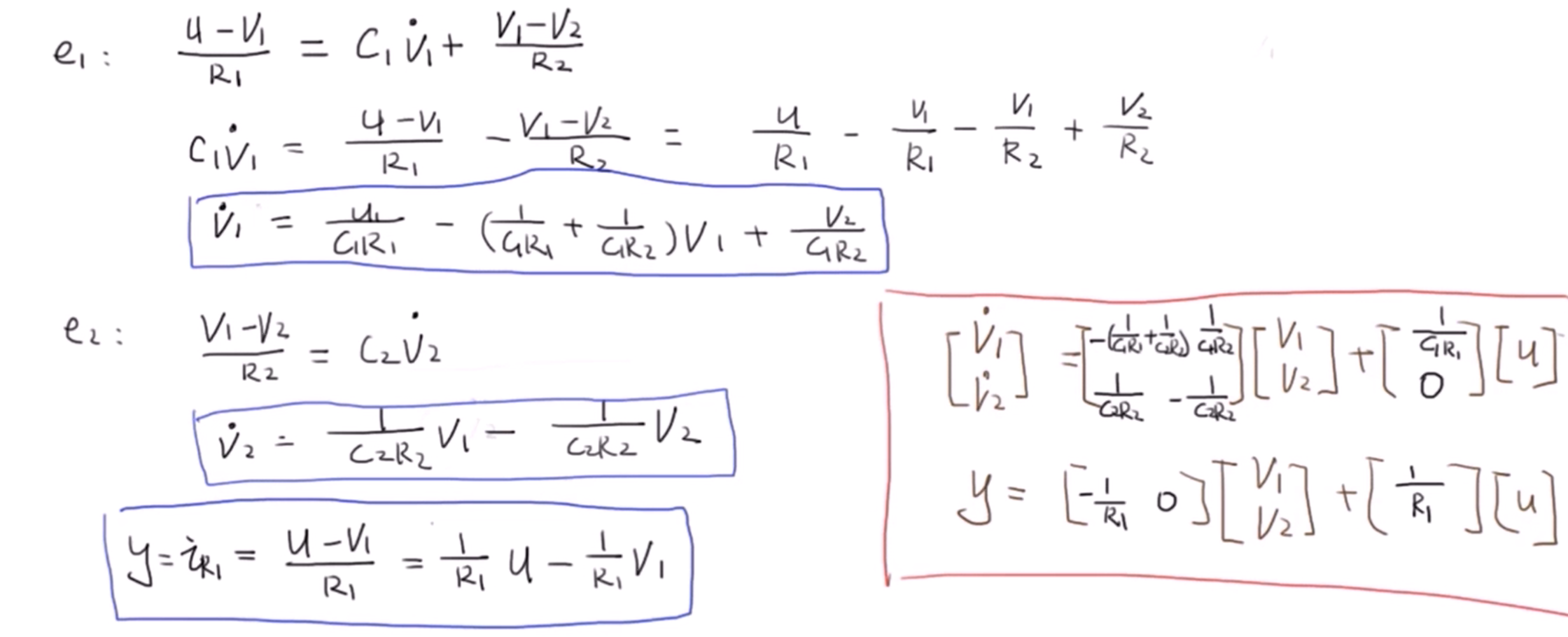
3 一个RC电路的例子