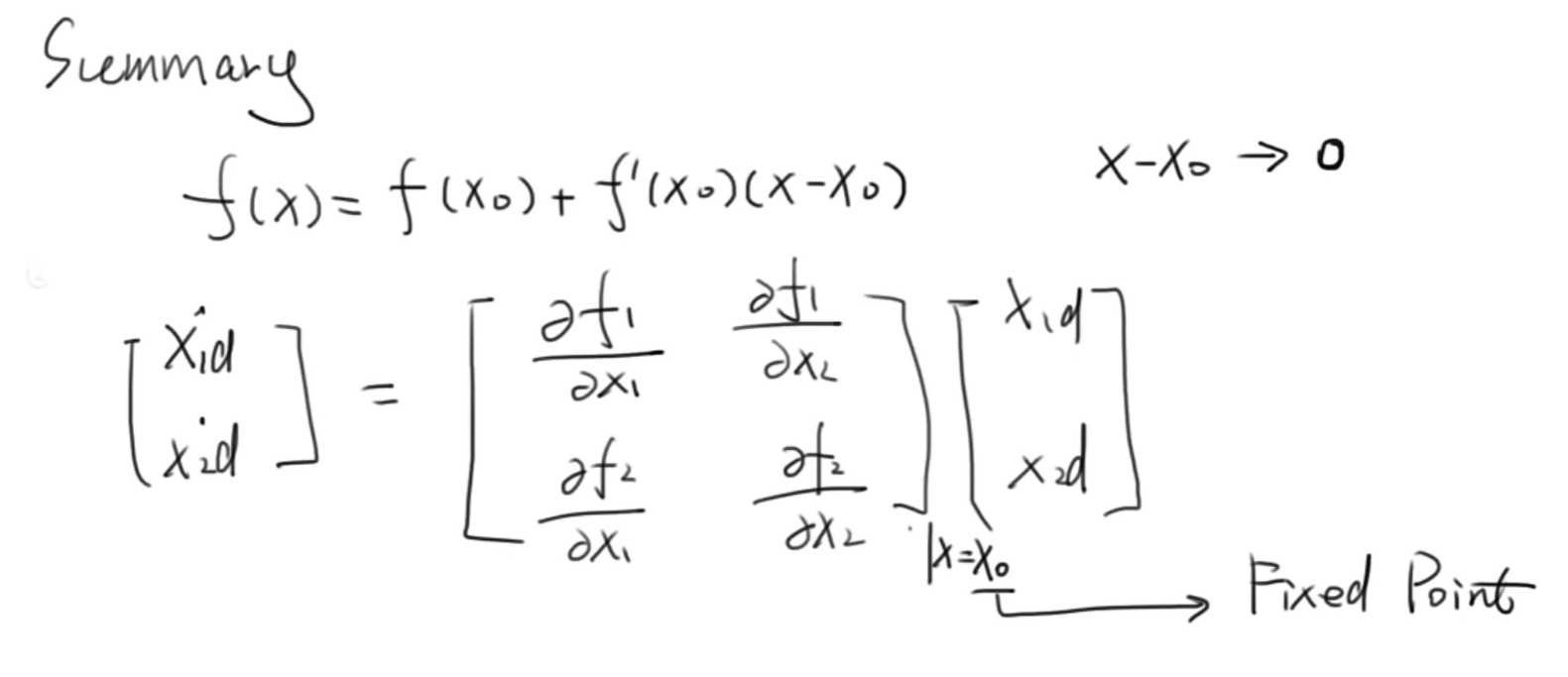该系列为DR_CAN工程数学基础系列视频笔记,详见https://space.bilibili.com/230105574
由于笔者水平有限,文中难免存在一些不足和错误之处,诚请各位批评指正。
1 定义
数学上的线性化(linearization)是找函数在特定点的线性近似,也就是函数在该点的一阶泰勒级数。在动力系统研究中,线性化是分析非线性微分方程系统或是非线性离散系统,在特定平衡点局部稳定性的一种方法。
2 线性系统
符合以下三点的系统我们称之为线性系统:

3 泰勒级数
泰勒级数是我们对微分方程进行线性化的重要工具。我们可以对函数 (f(x)) 使用泰勒级数展开到一阶,展开结果可以看作是一条直线:(k_2x+b) :
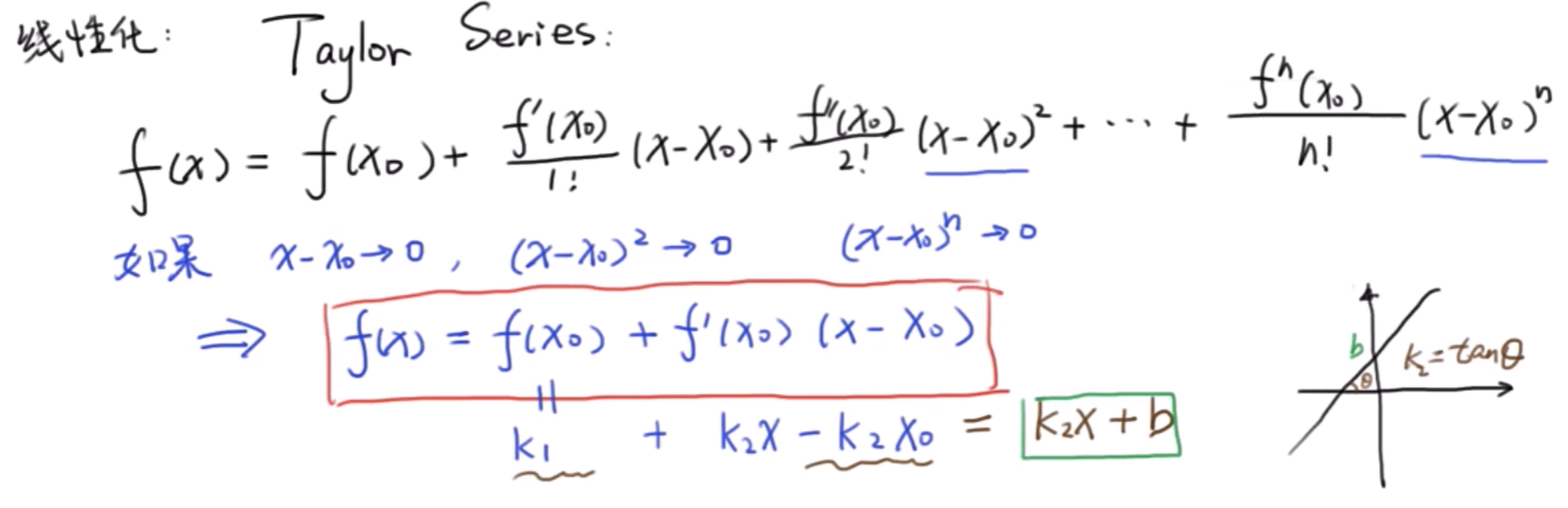
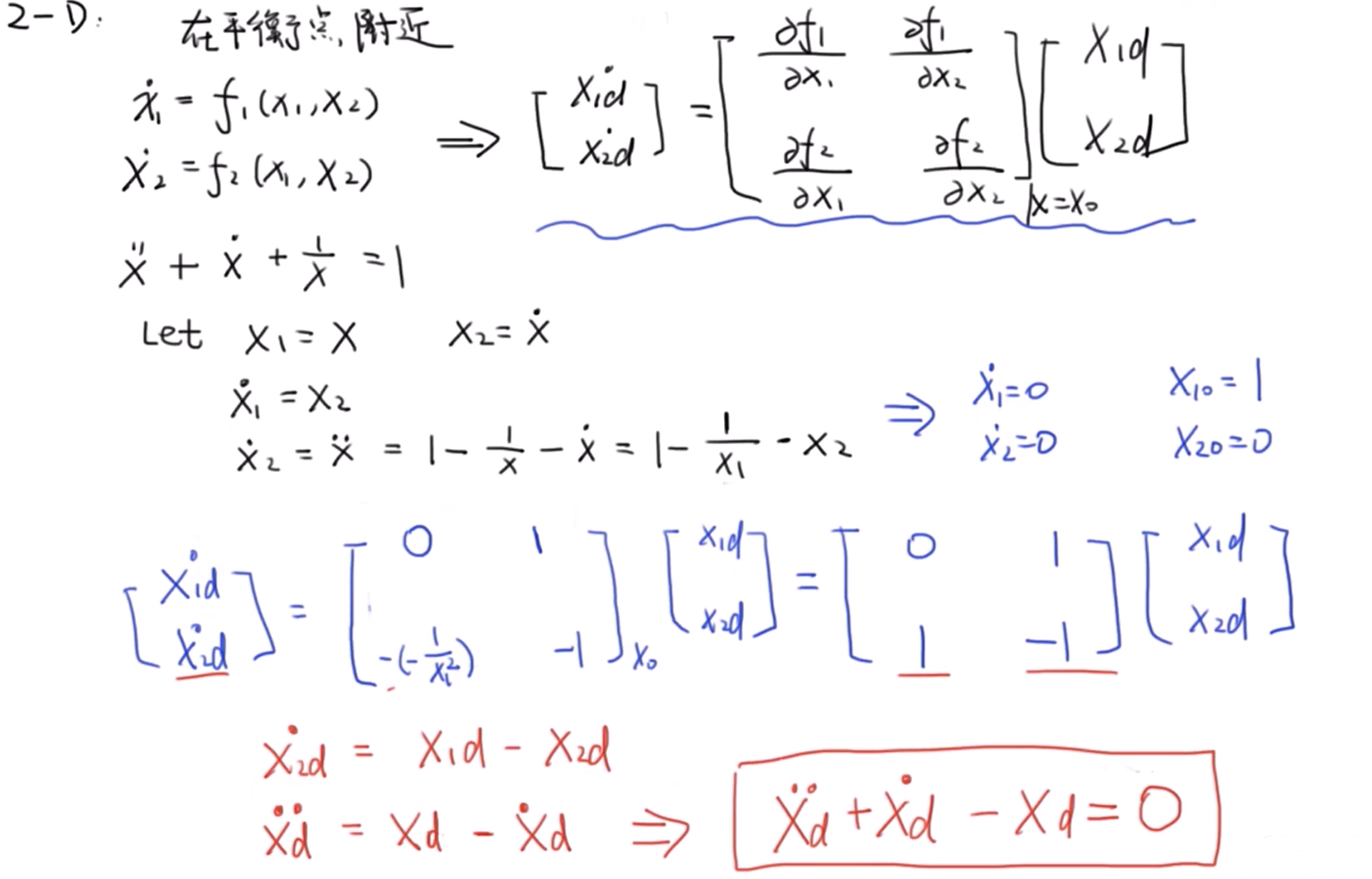
4 一维的例子
对于如下线性方程,我们在平衡点附近进行线性化。根据理论我们知道当一阶导二阶导均为0时系统是平衡点,因此代入可得平衡点 (x_0=1) 。我们把 (x_delta = x_0+x_d) 代入原微分方程,然后对 (frac{1}{x_delta}) 进行泰勒展开得到其平衡点的线性近似 (1-x_d) ,将结果带回微分方程 (ddot x_delta + dot x_delta +frac{1}{x_delta}=1) ,经过化简可得到线性化后的微分方程。注意的是这里的 (x_d) 并非以一开始的零点为零点,而是以平衡点 (x_0) 为零点:

5 状态空间的例子
与一维情况类似,首先找出平衡点,然后对向量进行泰勒展开,经过代入化简等方法可以得到和刚才相同的结果:
6 总结