点击这里可以跳转至
【1】矩阵汇总:http://www.cnblogs.com/HongYi-Liang/p/7287369.html
【2】矩阵生成:http://www.cnblogs.com/HongYi-Liang/p/7275278.html
【3】矩阵加减:现在的位置
【4】矩阵点乘:http://www.cnblogs.com/HongYi-Liang/p/7287324.html
【5】矩阵化简:http://www.cnblogs.com/HongYi-Liang/p/7464850.html
C++语言:
原理解析:
本节介绍矩阵与矩阵间的加法和减法,两个行列数相同的矩阵相加,把的矩阵对应的元素分别相加 。两个行列数相等矩阵相减,把矩阵的对应元素分别相减。
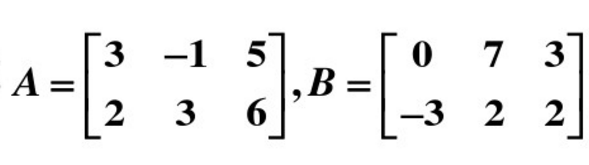
A+B=

矩阵加法:
首先需要判断矩阵是否行列数相等,在计算中,由于存放矩阵m_vecMatrix我们使用的是二维vector,所以我们需要:
- 判断合法性
- 把两个矩阵的第i行元素提取出来
- 把两个矩阵中此行的第j个元素提取并相加,推入一个临时向量tempVec中,
- 通过addOneRowToBack()函数将tempVec加入目标向量的m_vecMatrix(矩阵数据区)中
template <typename T> Matrix<T> Matrix<T>::operator+(Matrix<T> &matrix) //运算符重载“+”为矩阵加法 { /*matrix leagality check*/ if(this->m_iRows != matrix.getRows() || this->m_iColumns != matrix.getColumns()) { return *this; } Matrix<T> outputMatrix; vector<T> tempVec; for(int i=0;i<this->m_iRows;i++) { tempVec.clear(); for(int j=0;j<this->m_iColumns;j++) { tempVec.push_back(this->m_vecMatrix[i][j] + matrix.m_vecMatrix[i][j]); } outputMatrix.addOneRowToBack(tempVec); } return outputMatrix; }
矩阵减法:
矩阵减法与加法类似,我们只需要将上述过程赋值一遍,把"+"改为“-”。
template <typename T> Matrix<T> Matrix<T>::operator-(Matrix<T> &matrix) //运算符重载“-”为矩阵减法 { /*matrix leagality check*/ if(this->m_iRows != matrix.getRows() || this->m_iColumns != matrix.getColumns()) { return *this; } Matrix<T> outputMatrix; vector<T> tempVec; for(int i=0;i<this->m_iRows;i++) { tempVec.clear(); for(int j=0;j<this->m_iColumns;j++) { tempVec.push_back(this->m_vecMatrix[i][j] - matrix.m_vecMatrix[i][j]); } outputMatrix.addOneRowToBack(tempVec); } return outputMatrix; }