[Codeforces566C] Logistical Questions

一棵 (n) 个节点的树，点有点权，边有边权。求这棵树的一个点 (r) 使下面的式子最小：

[sum_{i in Tree} val_i imes dist(i, r)^{frac32} ]

(n le 2 imes 10^5, val_i, dist(u, v) ge 0)。

带权重心问题，有点妙。

设

[f(x) = sum_{i in Tree} val_i imes dist(i, x)^{frac32} ]

这里函数 (f) 的定义域是整棵树（不仅包括原来的点，还包括边上的点 ）。

下面研究这个函数的性质。

树上的函数显然不太方便研究，所以考虑换一个 (R) 上的函数研究。

随便选择一条树上路径 (u ightarrow v) 作为 (x) 轴，把 (u) 当作原点，这样 (x) 就是路径上的点到 (u) 的距离。

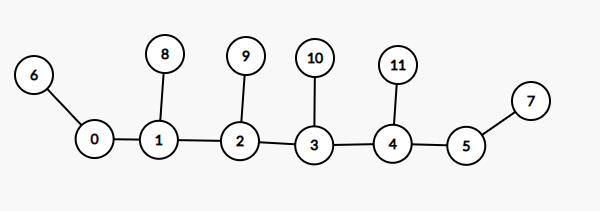
这里以 (0 ightarrow 5) 为例，节点 (6 dots 11) 分别代表其父亲的一些子树。

记 (d_i = dist(i, 0))，路径上的点分别考虑贡献：

[f_i(x) = egin{cases} sum_{c in subtree(i)} val_ileft (dist(i, c) + d_i - x ight)^frac32 & x le d_i\ sum_{c in subtree(i)} val_ileft(dist(i, c) + x - d_i ight)^frac32 & x > d_i end{cases}\ f(x) = f_0(x) + f_1(x) + f_2(x) + f_3(x) + f_4(x) + f_5(x) ]

发现 (f_i(x)) 可以写成下面这种形式（其中 (c_1-x ge 0, c_2 + x ge 0)）

[f_i(x) = egin{cases} sum v(c_1 - x)^frac32 & x le d_i\ sum v(c_2 + x)^frac32 & x > d_i end{cases} ]

求导（这里分段函数的分界点处显然可导）

[f_i'(x) = egin{cases} -frac32sum v(c_1 - x)^frac12 & x le d_i\ frac32sum v(c_2 + x)^frac12 & x > d_i end{cases} \ f_i''(x) = egin{cases} frac34sum v(c_1 - x)^{-frac12} & x le d_i\ frac34sum v(c_2 + x)^{-frac12} & x > d_i end{cases} ]

发现 (f''_i(x) ge 0)，所以 (f''(x) = sum_if''_i(x) ge 0)，所以 (f(x)) 是个凸函数，至多一个最小值。

注意到对于树上任意路径这个结论都成立，所以固定起点 (u)，对于所有终点 (v) 求一次最小值就可以得到答案。

下图中 (2, 3, 4) 都代表子树，假设当前在 (1) ，需要考虑 (1 ightarrow 2, 3, 4 ightarrow dots) 几种路径。

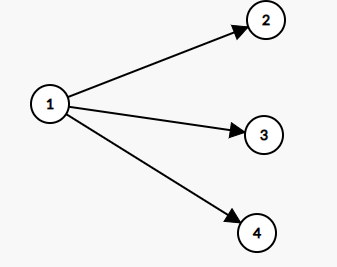
对于路径 (1 ightarrow i ightarrow dots)，有

[egin{aligned} f'(0)_i &= frac32left(sum_{xin 0} val_xdist(x, 1)^frac12 - sum_{xin i}val_xdist(x, 1)^frac12 ight)\ &= frac32left(sum_{x}val_xdist(x, 1)^frac12 - 2sum_{xin i}val_xdist(x, 1)^frac12 ight) end{aligned} ]

观察这个式子，发现最多只有一个 (i) 会使导数小于零，就是使 (sum_{x in i}val_xdist(x, i)^{frac12}) 最大的那个。

所以我们只需要向导数小于零的那个方向走就可以了。

假如从根出发向叶子的方向走，最多走 (maxdep) 次，每次需要花 (O(n)) 时间计算答案和导数， 最坏是 (O(n^2)) 的，考虑优化。

每次走到一个节点时，需要考虑的节点范围会缩小到当前节点的子树内，如果每次找到当前子树的重心，每次规模会减半，这样最多走 (log n) 次，最终复杂度 (O(n log n))。

#include <bits/stdc++.h>

template <class T, class U>
inline bool smin(T &x, const U &y) { return y < x ? x = y, 1 : 0; }
template <class T, class U>
inline bool smax(T &x, const U &y) { return x < y ? x = y, 1 : 0; }

constexpr int N(2e5 + 5);
int n, a[N], head[N];
struct Edge {
  int v, w, next;
} e[N << 1];
void addEdge(int x, int y, int z) {
  static int c = 0;
  e[++c] = { y, z, head[x] }, head[x] = c;
  e[++c] = { x, z, head[y] }, head[y] = c;
}
bool vis[N];
int rt, tSize, mSize, siz[N];
void getSize(int x, int fa) {
  siz[x] = 1;
  for (int i = head[x]; i; i = e[i].next) {
    int y = e[i].v;
    if (y == fa || vis[y])  continue;
    getSize(y, x);
    siz[x] += siz[y];
  }
}
void findrt(int x, int fa) {
  int max = tSize - siz[x];
  for (int i = head[x]; i; i = e[i].next) {
    int y = e[i].v;
    if (y == fa || vis[y]) continue;
    findrt(y, x);
    smax(max, siz[y]);
  }
  if (smin(mSize, max)) rt = x;
}
double ans = INFINITY, f, diff;
int pos;
void dfs(int x, int fa, int d) {
  f += a[x] * sqrt(d) * d, diff += a[x] * sqrt(d);
  for (int i = head[x]; i; i = e[i].next) {
    int y = e[i].v;
    if (y == fa) continue;
    dfs(y, x, d + e[i].w);
  }
}
void solve(int x) {
  if (vis[x]) return;
  vis[x] = 1;
  int p;
  double s = 0, m = 0;
  f = 0;
  for (int i = head[x]; i; i = e[i].next) {
    int y = e[i].v;
    diff = 0;
    dfs(y, x, e[i].w);
    if (smax(m, diff)) p = y;
    s += diff;
  }
  if (smin(ans, f)) pos = x;
  if (m * 2 > s && !vis[p]) {
    getSize(p, 0);
    tSize = mSize = siz[p];
    findrt(p, 0);
    solve(rt);
  }
}
int main() {
  std::ios::sync_with_stdio(false);
  std::cin.tie(nullptr);
  std::cin >> n;
  for (int i = 1; i <= n; i++) std::cin >> a[i];
  for (int i = 1, x, y, z; i < n; i++) {
    std::cin >> x >> y >> z;
    addEdge(x, y, z);
  }
  getSize(1, 0), tSize = mSize = n, findrt(1, 0), solve(rt);
  printf("%d %.10f", pos, ans);
  return 0;
}