上一篇中写了选择排序和插入排序,都是O(N^2)级别的,这篇将要实现的归并排序和快速排序都是O(Nlog(N))级别的。
归并排序
思路;首先将要排序的数组分成两部分,left_part,right_part,之后将排好序的left_right和right_part归并起来,同原始数组一样,被分成的Left_part,和right_part分别排序,而left_part 和right_part又可以分别分成left_part和right_part,这样不断递归,分到最后,left_part和right_part只有一个元素了,这时候不用排序了,因为它们本身就是有序的,我们将它们归并到上一级,上一级同样归并到更高的层级,直到归并到最后一个层级,所有元素变成有序的。
算法时间复杂度;我们每次将数组中的元素二分,最终我们会分多少次呢呢,我们可以想象一颗有n个节点的二叉树,这棵树的高度为log2(N),而每一层我们处理的元素的个数依然是N,总共处理log(N)层,所以O(N)= nlog(N),但同时,我们也发现,归并排序不像选择排序和插入排序那样可以在原数组上通过比较和交换完成(即就地排序),归并排序需要申请一段与要排序数组大小相同的空间辅助我们完成归并过程
这里,我用网上的图片简单说一下归并过程
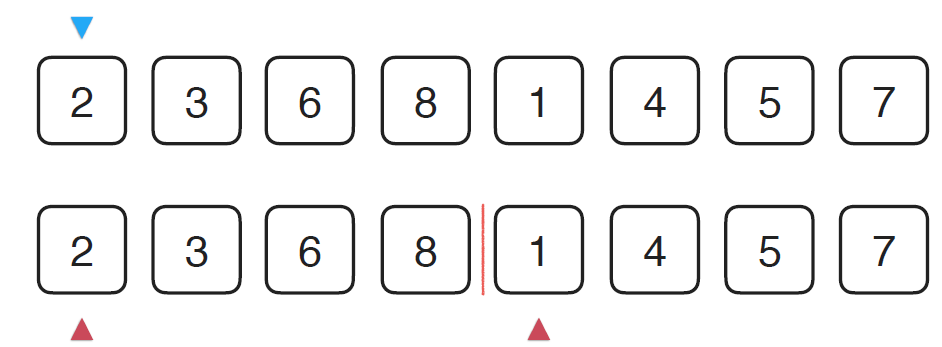
由图可以看出需要三个索引来完成,其中,蓝色表示在归并过程中,最终我们需要跟踪的位置,两个红色的分别指向两个已经排好序的数组当前要考查的元素。首先,比较left_part和right_part中红色指向的元素,1小于2,所以将1放在蓝色指向 的位置,蓝色箭头后移,同时,1所在的part中的红色箭头也要后移,left_part中的2与right_part中的4比较,2更小,将2放在蓝色箭头指向的位置,蓝色箭头后移,2所在part中的红色箭头后移,以此类推,直到有一部分所有元素都考察完,那么还有剩余元素的部分的剩下的元素全部放进蓝色箭头所在位置直到数组结束。所以归并过程实现如下,在实现之前,先说明一下:红色箭头指向的位置分别用i,j表示,蓝色箭头指向的位置用k表示,这里还需要注意,红色箭头表示的当前正在考察的元素,而蓝色箭头指向的位置表示的是两个部分比较后,应该放到的归并数组的位置,即不是归并结束后已经放置的最后一个元素位置,而是下一个需要放的位置。代码如下:
1 // merge for arr[l...mid] and arr[mid+1...r] 2 void merge(int arr[],int l,int mid,int r){ 3 int aux[r-l+1]; 4 for(int i = l;i<=r;i++) 5 //aux[i] = arr[i+l]; 6 aux[i-l] = arr[i]; 7 int i = l,j = mid+1; 8 for(int k = l;k<=r;k++){ 9 if(i>mid){ 10 arr[k] = aux[j-l]; 11 j++; 12 } 13 else if(j>r){ 14 arr[k] = aux[i-l]; 15 i++; 16 } 17 else if(aux[i-l]<aux[j-l]){ 18 arr[k] = aux[i-l]; 19 i++; 20 } 21 else{ 22 arr[k] = aux[j-l]; 23 j++; 24 } 25 } 26 }
merge sort 实现就如下了:
1 merge_sort(int arr[],int n){ 2 __merge_sort(arr,0,n-1); //start with —__:private 3 } 4 5 // merge sort for arr[l...r] 6 __merge_sort(int arr[],int l,int r){ 7 if(l>=r) 8 return; 9 int mid = (r-l)/2+l; 10 __merge_sort(arr,l,mid); 11 __merge_sort(arr,mid+1,r); 12 merge(arr,l,mid,r); 13 }
优化
上面的归并排序算法中,我们可以看到,不管将要归并的两部分的顺序如何,我们都进行了归并操作,这对于近乎有序的数组来说,其实是不必要的操作,所以,我们在归并操作前可以加一个判断条件;但既然优化操作是针对顺序性良好的数组的,那么我么也可以考虑在数组规模不是很大的情况下使用插入排序,上篇中提到,对于有序数组,插入排序可以达到线性级别。实现如下:
1 __merge_sort_opti(int arr[],int l,int r){ 2 if(r-l<15){ 3 insertion_sort(arr,l,r);// can realize this insertion_sort vertion 4 return; 5 } 6 int mid = (r-l)/2+l; 7 __merge_sort_opti(arr,l,mid); 8 __merge_sort_opti(arr,mid+1,r); 9 if(arr[mid]>arr[mid+1]) // only merge for the 10 merge(arr,l,mid,r); //arr[mid]>arr[mid+1]; 11 } 12 13 void merge_sort_opti(int arr[],int n){ 14 __merge_sort_opti(arr,0,n-1); 15 }
上面的归并排序是一种自顶向下的归并过程,那么自底向上的归并呢
还是以上面8个元素的那个数组为例,最初是每一个元素都是一段,向上归并,就变成了两个元素一段,继续向上归并,4个元素一段,直到最后8个元素一段,完成排序,这个过程,我们不需要递归,迭代就可以实现、
1 oid mergeSortBottomUp(int arr[],int n){ 2 //sz:size of merge,number of elementes need been merged 3 //sz starts with 1,doubled for each round merge 4 for(int sz =1;szsz<=n;sz+=sz){ 5 //first round arr[0...sz-1] and arr[sz...2*sz-1] 6 //second round arr[2*sz,3*sz-1] and arr[3*sz...4*sz-1] 7 // until up 8 for(int i = 0;i+sz<n;i+=sz+sz){ 9 //merge(arr,i,i+sz-1,i+sz+sz-1); 10 merge(arr,i,i+sz-1,min(i+sz+sz-1,n-1)); 11 } 12 }
也可以像自顶向下那样使用同样的方式进行优化,是一样的,就不重复了,下面实现快速排序