二叉搜索树的整理

二叉搜索树满足以下性质：

    1.若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 

    2.若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 

    3.它的左、右子树也分别为二叉排序树。

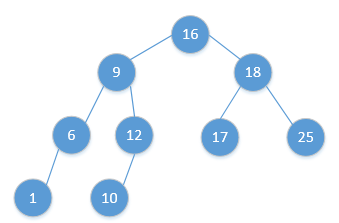
对于一个序列任意排序形成的二叉搜索树，中序遍历的结果唯一。

 

二叉搜索树的名词：

    1.键值：节点的数据

    2.前驱：比当前节点大的最小节点

    3.后继：比当前节点小的最大节点

 

二叉搜索树的基本操作：

    1.插入：比较插入点和当前点的键值，如果插入点小，递归当前点的左孩子，反之递归当前点的右孩子；

    2.搜索：比较输入值和当前点的键值，如果输入值小，递归当前点的左孩子，反之递归当前点的右孩子；

    3.删除：被删除节点的子树所具有的前驱具有比该节点的所有左子节点大且比该节点的所有右子节点小的性质，那么前驱可以直接代替被删除节点；同理，被删除节点的后继也具有同样的性质，也可以用来代替被删除节点；

    删除节点的分类讨论：

        (1) 存在前驱，则用前驱代替被删除节点；

        (2) 不存在前驱，存在后继，则用后继代替被删除节点；

        (3) 既不存在前驱，也不存在后继，即被删除节点没有子节点，直接将其父节点指向本身的指针删除；

    删除节点的步骤：

        /*假设被删除节点为s，用于替换的节点为z*/

        (1) 如果z有子节点，将z子节点指向z的父节点；否则，修改z父节点指向z的指针为NULL；

        (2) 将s的左孩子修改为z的左孩子，s的右孩子修改为z的右孩子；

        (3) 将z的父节点指向s的父节点；如果父节点为NULL，修改z为根节点；

 

数组模拟指针实现

 

const int maxn = 1e5+7;
struct node{
    int data,pos,lchild,rchild;
    bool exi;
}a[maxn];
int n = 0;

void insert(node key,int cur)
{
    if(key.data < a[cur].data)
    {
        if(a[cur].lchild) insert(key,a[cur].lchild);
        else a[cur].lchild = key.pos;
    }
    else
    {
        if(a[cur].rchild) insert(key,a[cur].rchild);
        else a[cur].rchild = key.pos;
    }
}

void insert(int key)
{
    a[++n].data = key;
    a[n].pos = n;
    a[n].lchild = a[n].rchild = 0;
    a[n].exi = true;
    insert(a[n],1);
}

void inOrder(int cur)
{
    if(a[cur].lchild) inOrder(a[cur].lchild);
    if(a[cur].exi) cout << a[cur].data << " " ;
    if(a[cur].rchild) inOrder(a[cur].rchild);
}

int search(int key)
{
    int cur = 1;
    while(cur && (key != a[cur].data || !a[cur].exi))
        cur = (key > a[cur].data) ? a[cur].rchild : a[cur].lchild ;
    return  cur;   //搜索失败返回0
}

void remove(int key)
{
    if(!key) return ;
    int l = a[key].lchild, r = a[key].rchild;
    if(l)
    {
        while(a[l].rchild)
            l = a[l].rchild;
        a[key].data = a[l].data;
        a[l].exi = false;
    }
    else if(r)
    {
        while(a[r].lchild)
            r = a[r].lchild;
        a[key].data = a[r].data;
        a[r].exi = false;
    }
    else a[key].exi = false;
}

int main()
{
    int arr[] = {5,1,2,9};
    n = 4;  //size
    
    for(int i=1;i<=n;i++)   //initial
    {
        a[i].pos = i;
        a[i].data = arr[i-1];
        a[i].lchild = a[i].rchild = 0;
        a[i].exi = true;
    }
    
    for(int i=1;i<=n;i++)   //create
    {
        insert(a[i],0);
    }
    
    inOrder(0);
    cout << endl;
    
    insert(7);   //insert
    
    inOrder(0);
    cout << endl;
    
    cout << "lchild: " <<a[a[search(5)].lchild].data << " " << "rchild: " << a[a[search(5)].rchild].data << endl;   //search
    
    remove(search(5));   //delete
    
    inOrder(0);
    cout << endl;
    
    insert(5);   //reinsert
    
    inOrder(0);
    cout << endl;
}

 

二叉搜索树类（指针实现）

 

二叉搜索树的节点结构：

struct Binode{
    int data;
    Binode *lchild,*rchild,*parent;
    Binode(int _data,Binode *_l,Binode *_r,Binode *_p):data(_data),lchild(_l),rchild(_r),parent(_p){}
};

头文件：

#ifndef BSTree_h
#define BSTree_h

struct Binode{
    int data;
    Binode *lchild,*rchild,*parent;
    Binode(int _data,Binode *_l,Binode *_r,Binode *_p):data(_data),lchild(_l),rchild(_r),parent(_p){};
};

class BSTree{
    Binode * root;
    
public:
    BSTree(Binode * _root = NULL):root(_root){}
    
    void insert(int key);
    
    void insert(Binode * &tree,Binode * s);
    
    void inOrder();
    
    void inOrder(Binode *_root);
    
    Binode *search(int key);
    
    Binode *minNode();
    
    Binode *maxNode();
    
    int minKey();
    
    int maxKey();
    
    Binode *predecessor(Binode *now);
    
    Binode *predecessor(int key);
    
    Binode *sucessor(Binode *now);
    
    Binode *sucessor(int key);
    
    void deleteNode(int key);
    
    void deleteNode(Binode *&s);
    
};

#endif /* BSTree_h */

cpp：

#include <stdio.h>
#include "BSTree.h"

void BSTree::insert(int key)
{
    Binode *temp = new Binode(key,NULL,NULL,NULL);
    insert(root,temp);
}

void BSTree::insert(Binode * &tree,Binode *s)
{
    Binode *parent = NULL;
    Binode *temp = tree;
    while(temp != NULL)
    {
        parent = temp;
        if(s->data > temp->data)
            temp = temp->rchild;
        else temp = temp->lchild;
    }
    s->parent = parent;
    if(parent == NULL)
        root = s;
    else if(s->data > parent->data)
        parent->rchild = s;
    else parent->lchild = s;
}

void BSTree::inOrder()
{
    inOrder(root);
}

void BSTree::inOrder(Binode *_root)
{
    if(_root == NULL) return ;
    else
    {
        inOrder(_root->lchild);
        printf("%d ",_root->data);
        inOrder(_root->rchild);
    }
}

Binode *BSTree::search(int key)
{
    Binode *temp = root;
    while(temp != NULL && temp->data != key)
    {
        if(temp->data > key)
            temp = temp->lchild;
        else temp = temp->rchild;
    }
    return temp;
}

Binode *BSTree::minNode()
{
    Binode *temp = root;
    while(temp->lchild != NULL)
        temp = temp->lchild;
    return temp;
}

Binode *BSTree::maxNode()
{
    Binode *temp = root;
    while(temp->rchild != NULL)
        temp = temp->rchild;
    return temp;
}

int BSTree::minKey()
{
    return minNode()->data;
}

int BSTree::maxKey()
{
    return maxNode()->data;
}

Binode *BSTree::predecessor(int key)
{
    Binode *now = search(key);
    if(now == NULL)
        return NULL;
    else return predecessor(now);
}

Binode *BSTree::predecessor(Binode *now)
{
    if(now->lchild != NULL)
    {
        Binode *temp = now->lchild;
        while(temp->rchild != NULL)
            temp = temp->rchild;
        return temp;
    }
    else if(now->parent->rchild == now)
        return now->parent;
    else return NULL;
}

Binode *BSTree::sucessor(int key)
{
    Binode *now = search(key);
    if(now == NULL) return NULL;
    else return sucessor(now);
}

Binode *BSTree::sucessor(Binode *now)
{
    if(now->rchild != NULL)
    {
        Binode *temp = now->rchild;
        while(temp->lchild != NULL)
            temp = temp->lchild;
        return temp;
    }
    else if(now->parent->lchild == now)
        return now->parent;
    else return NULL;
}

void BSTree::deleteNode(int key)
{
    Binode *s = search(key);
    if(s != NULL)
        deleteNode(s);
    delete s;
}

void BSTree::deleteNode(Binode *&s)
{
    Binode *l = s->lchild;
    Binode *r = s->rchild;
    if(l)
    {
        while(l->rchild != NULL)
            l = l->rchild;
        if(l->lchild)
        {
            l->rchild->parent = l->parent;
            l->rchild->data > l->parent->data ? l->parent->rchild = l->lchild : l->parent->lchild = l->lchild;
        }
        l->parent->lchild == l ? l->parent->lchild = NULL : l->parent->rchild = NULL;
        l->lchild = s->lchild;
        l->rchild = s->rchild;
        if(l->lchild)l->lchild->parent = l;
        if(l->rchild)l->rchild->parent = l;
        if(s->parent) s->parent->lchild == s ? s->parent->lchild = l : s->parent->rchild = l;
        l->parent = s->parent;
        if(l->parent == NULL) root = l;
    }
    else if(r)
    {
        while(r->lchild != NULL)
            r = r->lchild;
        if(r->rchild)
        {
            r->lchild->parent = r->parent;
            r->lchild->data > r->parent->data ? r->parent->rchild = r->rchild : r->parent->lchild = r->rchild;
        }
        r->parent->lchild == r ? r->parent->lchild = NULL : r->parent->rchild = NULL;
        r->lchild = s->lchild;
        r->rchild = s->rchild;
        if(r->lchild)r->lchild->parent = r;
        if(r->rchild)r->rchild->parent = r;
        if(s->parent) s->parent->lchild == s ? s->parent->lchild = r : s->parent->rchild = r;
        r->parent = s->parent;
        if(r->parent == NULL) root = r;
    }
    else if(s->parent) s->parent->lchild == s ? s->parent->lchild = NULL : s->parent->rchild = NULL;
}