STL查找序列中处于某一大小范围内的元素个数

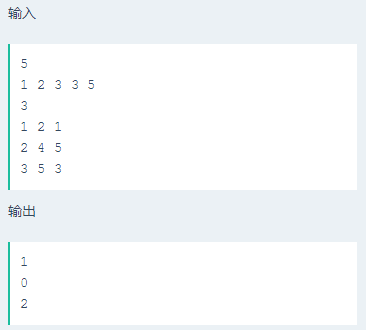
还是头条的笔试题（咦？），问题最后转换成这样的形式：

输入：不包含重复元素的有序数组a[N]以及上下界low, high;

输出：数组a[N]中满足元素处于闭区间[low,high]内（即low <= a[i] <= high）的元素个数

二分查找一向的特点，原理上非常好理解，但是判断边界的时候则是十分头疼。

这里我一开始都用lower_bound来查找low和high，返回两个位置it1，it2，然后计算初始数量cnt = it2 - it1 + 1;（因为是闭区间所以加1），然后再判断it1、it2找到的到底是low和high本身还是比它们大的数。

实际上不必这么麻烦，直接用lower_bound查找low，upper_bound查找high就行。

再回顾这两个函数：lower_bound返回的是第一个大于或等于查找值的迭代器，upper_bound返回的是第一个大于查找值的迭代器。

举个例子：int a[4] = { 3, 5, 7, 9 };分4种典型情况考虑

1、low=4,high=6。结果为1（元素5）。lower_bound(4)返回的是5的位置&a[1]，upper_bound(6)返回的是7的位置&a[2]，数量为2-1=1，无误；

2、low=4,high=7。结果为2（元素5、7）。lower_bound(4)返回的是5的位置&a[1]，upper_bound(7)返回的是9的位置&a[3]，数量为3-1=2，无误；

3、low=5,high=6。结果为1（元素5）。lower_bound(5)返回的是5的位置&a[1]，upper_bound(6)返回的是7的位置&a[2]，数量为2-1=1，无误；

4、low=5,high=7。结果为2（元素5、7）。lower_bound(5)返回的是5的位置&a[1]，upper_bound(7)返回的是9的位置&a[3]，数量为3-1=2，无误；

在此之上进行推广，假如low,high组成的不是闭区间，计算方法如下

至于笔试题的解法，代码如下：

#include <iostream>
#include <vector>
#include <unordered_map>
#include <algorithm>
using namespace std;

int main()
{
    // 输入
    int n;
    cin >> n;
    vector<int> val(n);
    for (int i = 0; i < n; i++)
    {
        cin >> val[i];
    }
    int q;
    cin >> q;
    // 构建hash表, key为以1开始的数组下标
    unordered_map<int, vector<int>> m;
    for (int i = 0; i < n; i++)
    {
        if (m.count(val[i]) == 0)
        {
            m.emplace(val[i], vector<int>{ i + 1 });
        }
        else
        {
            m[val[i]].emplace_back(i + 1);
        }
    }
    // 读取q组{l,r,k}, 输出m[k]中在区间[l,r]内的元素个数
    vector<int> l(q);
    vector<int> r(q);
    vector<int> k(q);
    for (int i = 0; i < q; i++)
    {
        cin >> l[i] >> r[i] >> k[i];
    }
    vector<int> res(q);
    for (int i = 0; i < q; i++)
    {
        int ll = l[i];
        int rr = r[i];
        int kk = k[i];
        if (m.count(kk) == 0)  // 喜好度为k的用户个数为0
        {
            res[i] = 0;
        }
        else
        {
            int cnt = 0;
            auto it1 = lower_bound(m[kk].begin(), m[kk].end(), ll);
            auto it2 = upper_bound(m[kk].begin(), m[kk].end(), rr);
            res[i] = it2 - it1;
        }
    }
    // 输出结果
    for (int x : res)
        cout << x << endl;
}