一. 递归
本质上,将原来的问题,转化为更小的同样的问题
举例:数组求和
Sum(arr[0... n-1]) = arr[0] + Sum(arr[1...n-1]) 第二部分为更小的同一个问题
Sum(arr[1...n-1]) = arr[1] + Sum(arr[2...n-1]) 第二部分为更小的同一个问题
......
Sum(arr[n-1 ... n-1]) = arr[n-1] + Sum([ ]) 第二部分为最基本的问题
//计算arr[l...n)范围里的数字和
private static int sum(int[] arr, int l){ if(l == arr.length) return 0; //a return arr[l] + sum(arr,l+1); //b }
a.求解最基本问题
b.把原问题转化为更小的问题
注意递归函数的“宏观”语意
递归函数就是一个函数。完成一个功能

二. 链表天然的递归性
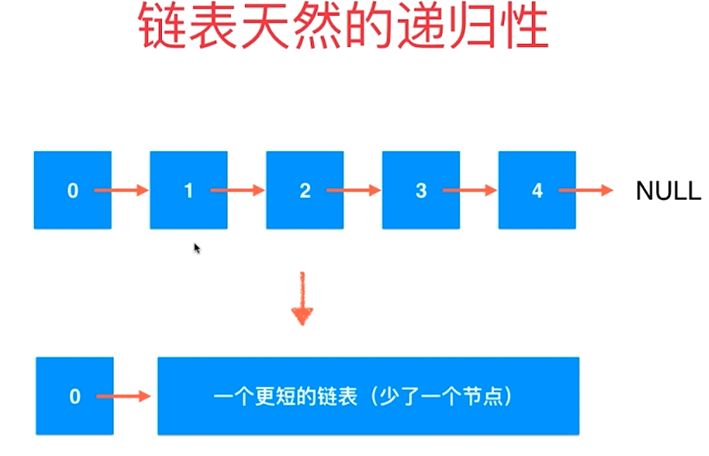
![]()
递归解决删除这个更小的链表中相应的元素
删除链表中所有值为value的节点
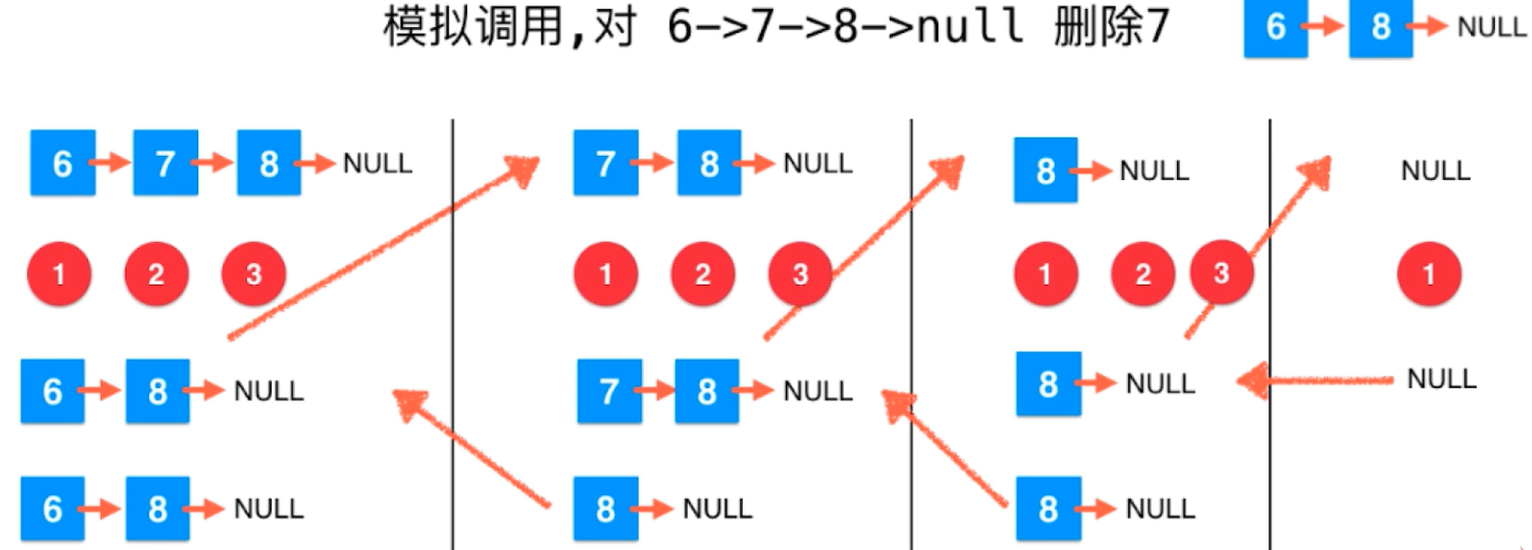
public ListNode removeElements(ListNode head, int val){ if(head == null){ return null; } ListNode res = removeElements(head.next, val); if(head.val == val){ return res; }else{ head.next = res; return head; } }
程序调用的系统栈
递归调用是有代价的:函数调用 + 系统栈空间
和链表相关的话题
递归
近乎和链表相关的所有操作,都可以使用递归的形式完成。
双向链表
循环链表
数组链表