74. 搜索二维矩阵
题目链接
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/search-a-2d-matrix/
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题目描述
编写一个高效的算法来判断 m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:
每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。
示例 1:
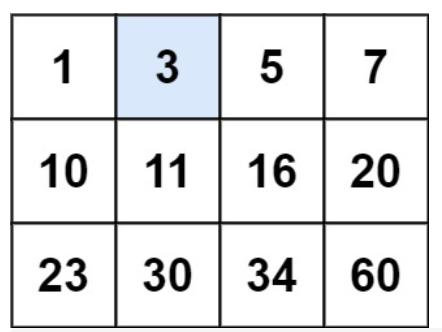
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出:true
示例 2:
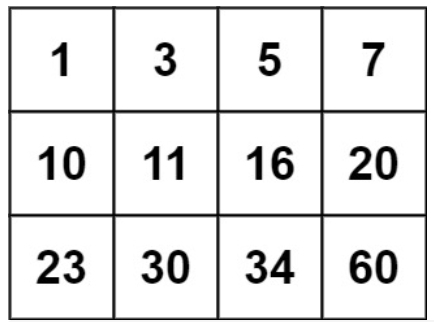
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出:false
提示:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 100
- -104 <= matrix[i][j], target <= 104
题目分析
- 根据题目描述在二维数组中查找指定元素
- 先查找target所处在的行号,使用顺序查找,建议使用二分查找
- 在target所属的行内使用二分查找target
代码
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int index = -1;
int left = 0;
int right = matrix[0].size() - 1;
for (int i = 0; i < matrix.size(); i++)
if (target >= matrix[i][left] && target <= matrix[i][right]) {
index = i;
break;
}
if (index < 0) return false;
while (left <= right) {
int mid = (left + right) / 2;
if (matrix[index][mid] > target) right = mid - 1;
else if (matrix[index][mid] < target) left = mid + 1;
else return true;
}
return false;
}
};