今天是被安排的cf。。。
我真的是太菜了啊。。。又双叒叕被机房的一群dalao吊打了。。。
这就是我与6年级的dalao的区别吗。。。
我裂开了
简单题。
就是把移动距离加起来就好了。。。
我居然能写错。。。真的是应该去开一道猪国杀写写。。。锻炼锻炼码力。。。
唉
T2:B - Composite Coloring
还是大水题。。。
可以发现。。。sqrt（100）是没有上34的。。。
没有上34的质数只有11个。。。
m<=11不就是最大的提示吗。。。
那就只要找一下质数，枚举每个数是否是他的倍数就好了啊。。。
我tm又卡了30分钟。。。淦，我裂开来
T3。。。C - K-Complete Word
我太难了
就是个极其明显的贪心。。
把每一位上的字符统计一下，选最多的就好了。。。
wtm没算是回文串。。。得到了比样例更优的解法。。。
直接原地爆炸。。。连调代码的希望都没了。。。
大水题。。。
直接构造一个2*3的矩阵就好了。。。
这就是通解。。。
他的代码不是dp，就是个贪心。。。
T5:
E - Height All the Same
这个要好好讲讲了。
题目大意就是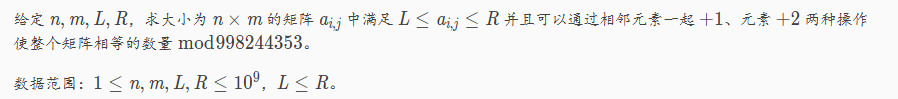
这个并没有那么好想。。。主要是我数学非常的不好。。。
其实对于数学学得好的人就是个大水题。
先来分析一下这道题目2种操作真正的含义
相邻的元素+1：使奇偶性变换，如（1,2）->（2,3），（奇，偶）->（偶，奇）
一个元素自己+2:奇偶性不变，仅仅是在填充。
为什么会想到奇偶性呢？
其实，+2与+1的题目，有很大的可能是有关于奇偶性的。只需要多写几道类似的题目就会有感觉了。
还有一个很必要的地方，就是这种操作无论怎么进行都不会影响到他的总和的奇偶性。
首先，我们用Even（E）来表示其中的偶数的个数，Odd（O）来表示其中奇数的个数。
接下来开始分类讨论
1.如果，n*m为奇数
这样分的原因是因为这种情况是一定有解的。
因为这意味着要么是E%2==0，要么是O%2==0
都是偶数个了，那么通过+1一定是能使他们全部变为一种情况的。
说明这一定有解。
2.如果，n*m为偶数
设最终堆叠了h层。
那么对于最终的答案，就是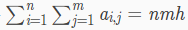
所以我们只需要保证这个为偶数，就可以保证最终答案的有解了。
为什么保证nmh%2==0就可以保证最终答案的有解了呢？
因为最终为偶数，就说明有偶数个O。
这就非常显然了。
那么，答案是什么呢?
设2i为奇数的位置数
这就是答案。
从没有奇数到每个位置都有奇数
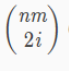为求每个状态中每个位置为奇数的情况。
O2iEnm-2i指的是每个位置对答案的贡献。
这些加起来就是答案了。
可是，这是一个暴力。。。
TLE稳稳的。
我们就需要对他进行化简，这样是我们列出这个式子真正的目的：优化。
看到这个就应该联想到二项式定理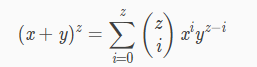
是不是非常的相似呢？
发现(O+E)nm的值就是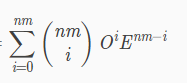
将奇数项与偶数项拉出来，得到
发现左边就是我们需要的答案。
右边这个式子怎么消掉呢？
把它在加上一个（O-E）nm就好了。（O-E）nm分解出来的式子其中一个正好消掉了。
再除以2就是我们需要的答案了。
所以！答案就是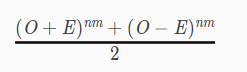
这种乘法直接使用快速幂就能够快速求解了
#include<bits/stdc++.h> #define MOD 998244353 #define ll long long using namespace std; ll T,n,m,l,r; inline ll read() { char c=getchar();ll a=0,b=1; for(;c<'0'||c>'9';c=getchar())if(c=='-')b=-1; for(;c>='0'&&c<='9';c=getchar())a=a*10+c-48; return a*b; } ll qpow(ll a,ll p) { ll res=1; if(a==0)return 0; while(p) { if(p&1)res=res*a%MOD; a=a*a%MOD; p>>=1; } return res; } int main() { n=read();m=read();l=read();r=read(); if(n*m&1) cout<<qpow((r-l+1)%MOD,n*m%(MOD-1))<<endl; else { ll E=(r>>1)-(l-1>>1); ll O=r-l+1-E; cout<<((qpow((O+E)%MOD,n*m%(MOD-1))+qpow((O-E+MOD)%MOD,n*m%(MOD-1)))*499122177%MOD)<<endl; } return 0; }
ok
这是dp。。。
只是状态有那么的一丁点难想。。。
淦啊，我看不懂题面。。。
不写了。。
//Data const int N=300000,m=998244353; int n; vector<lng> f[3]; vector<vector<int> > e; //Dfs il void Dfs(re int x,re int fa){ f[0][x]=f[1][x]=f[2][x]=1; for(re int to:e[x])if(to!=fa){ Dfs(to,x); (f[0][x]*=f[0][to])%=m; (f[1][x]*=(f[0][to]+f[1][to]+f[2][to]))%=m; (f[2][x]*=(f[0][to]+f[1][to]))%=m; } f[0][x]=(f[1][x]+f[2][x]-f[0][x]+m)%m; } //Main int main(){ scanf("%d",&n); e.resize(n+7); for(re int i=0;i<3;i++) f[i].resize(n+7); for(re int i=1,u,v;i<n;i++) scanf("%d%d",&u,&v),e[u].pb(v),e[v].pb(u); Dfs(1,0); printf("%lld ",(f[0][1]+m-1)%m); return 0; }
the end