1.卷积的认识
已有的运算:加减乘除,幂运算指数运算
卷积:卷积是一种运算
2.卷积运算
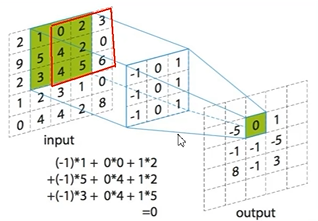
卷积操作是使用一个二维卷积核(3x3)在一个批处理的图片上不断扫描,具体操作就是将一个卷积核在每张图片上按照一个合适的尺寸在每个通道上面进行扫描
3.使用卷积的目的
卷积核,小卷积(3x3,5x5)本质当成系数,代码中用变量表示
卷积的目的就是提取特征
输入特征图的深度(channel数),决定了当前层卷积核的深度
由于每个卷积核在卷积计算后,会得到一张输出特征图,所以当前层使用了几个卷积核,就有几张输出特征图
当前层卷积核的个数,决定了当前层输出特征图的深度
通道数=卷积核数=卷积核的深度
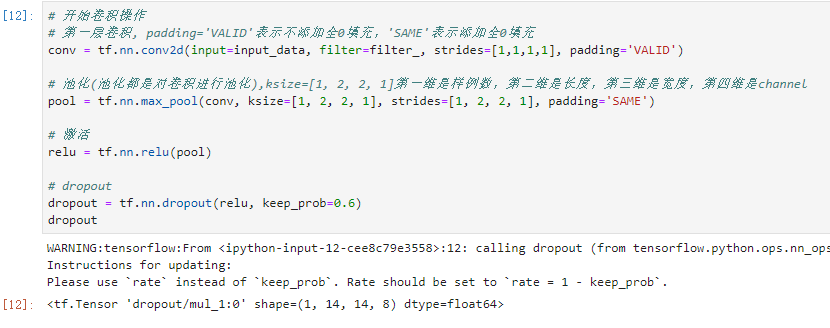
4.卷积构造方法
(1)激活函数
在神经网络中,激活函数的作用是能够给神经网络加入一些非线性因素,使得神经网络可以更好地解决较为复杂的问题
也就是说,神经网络中每一个神经元都非常简单,都是线性的,加入激活函数后,把它变成非线性的。
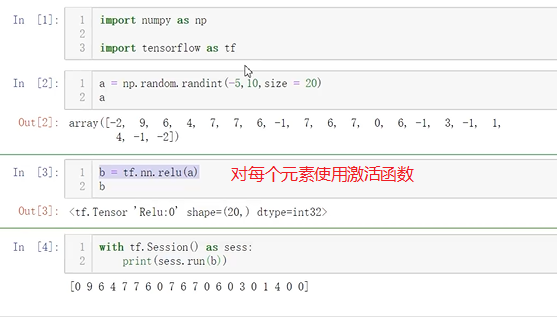
在神经网络中,我们有很多的非线性函数来作为激活函数,比如连续的平滑非线性函数(sigmoid, tanh和softplus),连续但不平滑的非线性函数(relu,relu6和relux)和随机正则化函数(dropout)
所有的激活函数都是单独应用在每个元素上面的,并且输出张量的维度和输入张量的维度一样(改变数据,不改变维度)
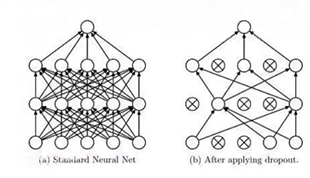
(2)Dropout
当训练数据量比较小时,可能会出现因为追求最小差值导致训练出来的模型极度符合训练集,但缺乏普适性,不能表达训练数据之外的数据(即过拟合)
解决过拟合问题:L1正则化,L2正则化,dropout是专门用在神经网络的正则化方法

def add_layer(inputs, in_size, out_size, layer_name, activation_function=None):
# add one more layer and return the output of this layer
Weights = tf.Variable(tf.random_normal([in_size, out_size]))
biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)
Wx_plus_b = tf.matmul(inputs, Weights) + biases
# here to dropout
Wx_plus_b = tf.nn.dropout(Wx_plus_b, keep_prob)
if activation_function is None:
outputs = Wx_plus_b
else:
outputs = activation_function(Wx_plus_b)
tf.summary.histogram(layer_name + '/outputs', outputs)
return outputs
# 这里的keep_prob是保留概率,即我们要保留的结果所占比例, # 它作为一个placeholder,在run时传入,当keep_prob=1的时候,相当于100%保留,也就是dropout没有起作用。 keep_prob = tf.placeholder(tf.float32)
(3)卷积层
卷积操作是使用一个二维卷积核(3x3)在一个批处理的图片上不断扫描,具体操作就是将一个卷积核在每张图片上按照一个合适的尺寸在每个通道上面进行扫描


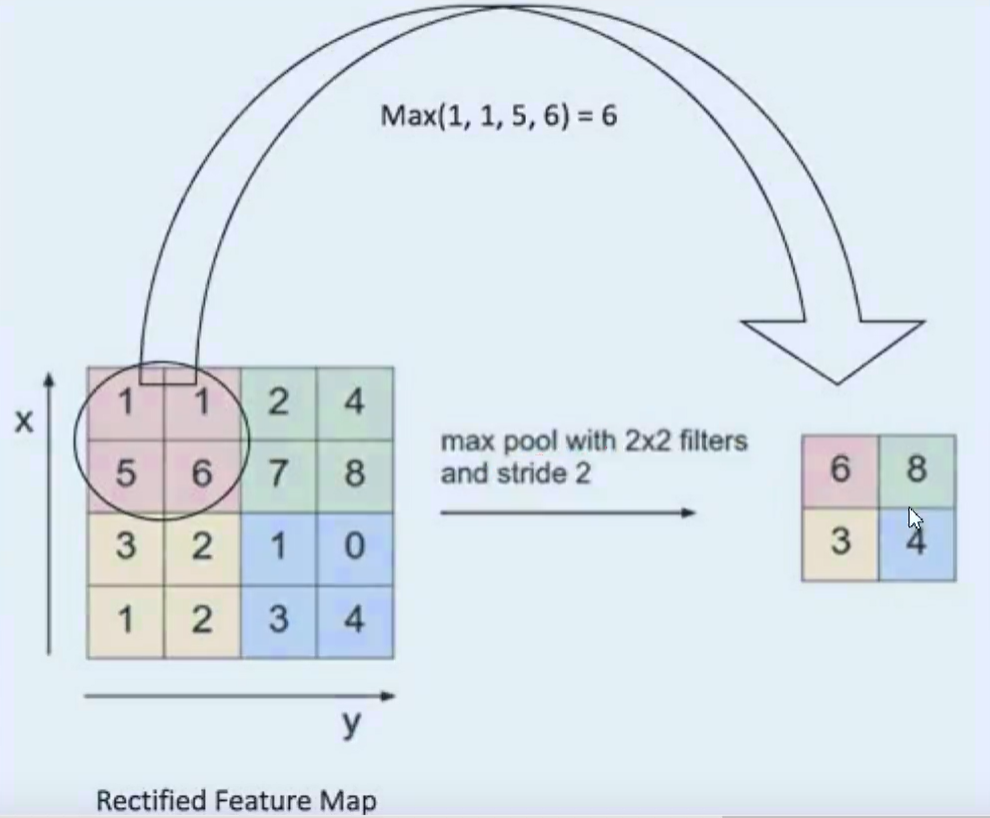
(4)池化层(筛选出重要特征)
池化层是对卷积层的处理,池化操作是利用一个矩阵窗口在输入张量上进行扫描,并且将每个矩阵窗口中的值通过取最大值,平均值或者xxxx来减少元素个数(减少元素个数相当于提取元素重要特征)
因为卷积的目的是提取特征,所有的特征都提取出来了,我们在研究一个东西时候,要看其关键特征
池化层可以非常有效地缩小矩阵尺寸,主要用于减小矩阵的长和宽
Maxpooling就是在这个区域内选出最能代表边缘的值,然后丢掉那么没多大用的信息,为什么这么做?
举个例子:
有四个美女,如果非要你选,你选谁?你肯定选最漂亮的(最符合的特征)

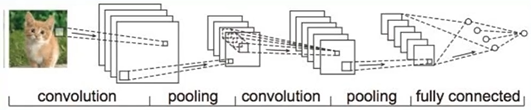
(5)全连接层(其实就是矩阵运算)
fully connected就是将卷积池化之后的数据变成能够进行矩阵运算的
四维数据转换成二维的
可以看到fully connected变成了一个一个神经元
(6)每一层都要给激活函数
卷积神经网络的构造:
1.卷积,提取特征
2.池化,筛选出最大的特征
3.激活,加入非线性
4.dropout防止过拟合
5.归一化操作
练习:
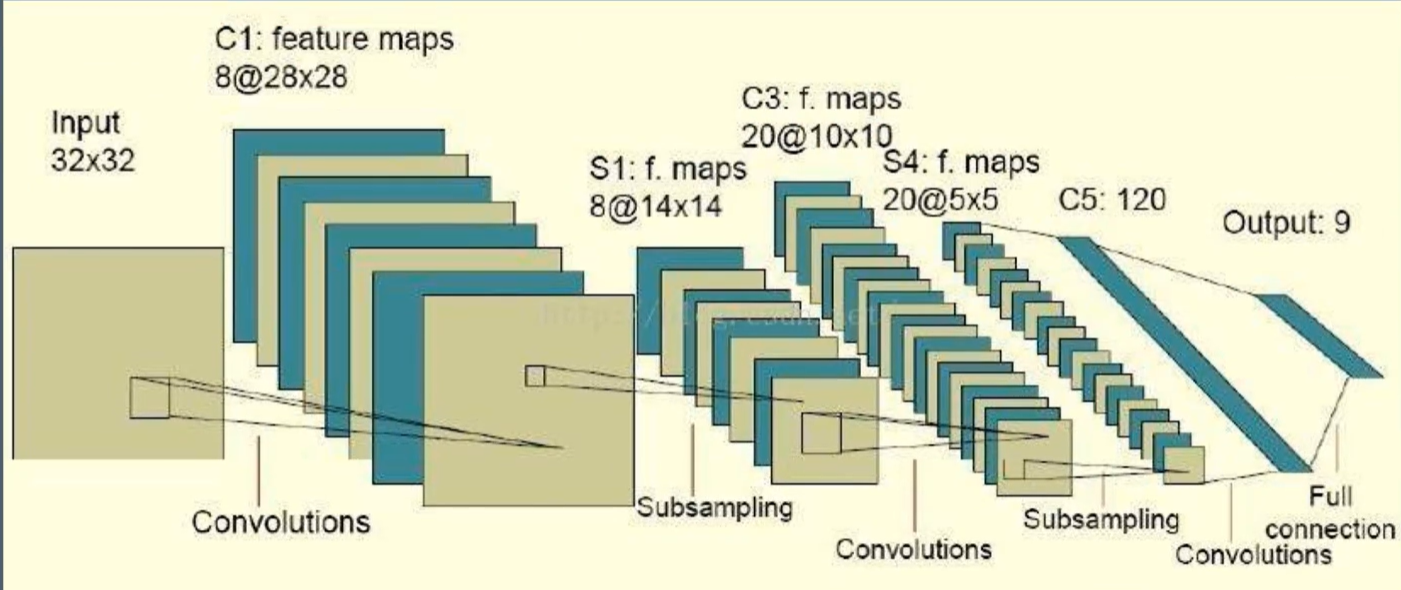
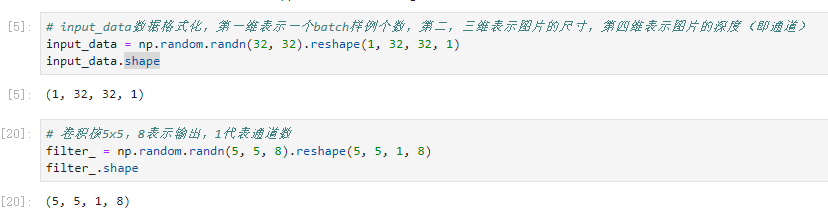
# tensorflow2.1.0+win10 import tensorflow.compat.v1 as tf tf.disable_v2_behavior() import numpy as np # input_data数据格式化,第一维表示一个batch样例个数,第二,三维表示图片的尺寸,第四维表示图片的深度(即通道) input_data = np.random.randn(32, 32).reshape(1, 32, 32, 1) # 卷积核5x5,8表示输出,1代表通道数 filter_ = np.random.randn(5, 5, 8).reshape(5, 5, 1, 8) # 开始卷积操作 # 第一层卷积, padding='VALID'表示不添加全0填充,'SAME'表示添加全0填充 conv = tf.nn.conv2d(input=input_data, filter=filter_, strides=[1,1,1,1], padding='VALID') # 池化(池化都是对卷积进行池化),ksize=[1, 2, 2, 1]第一维是样例数,第二维是长度,第三维是宽度,第四维是channel pool = tf.nn.max_pool(conv, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME') # 激活 relu = tf.nn.relu(pool) # dropout dropout = tf.nn.dropout(relu, keep_prob=0.6) # 第二层卷积 # 以第一层卷积的数据进行修改 filter2=np.random.randn(5, 5, 8, 20) #为什么是8?上一层的输出是8,为什么是20?本层输出是20 conv2 = tf.nn.conv2d(input=dropout, filter=filter2, strides=[1,1,1,1], padding='VALID') # 池化 pool = tf.nn.max_pool(conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME') # 激活 sigmoid = tf.nn.sigmoid(pool) #dropout dropout2 = tf.nn.dropout(sigmoid, keep_prob=0.5) # 全连接层, 其实是一个矩阵运算 dense = np.random.randn(500, 120) fc = tf.reshape(dropout2, shape=[1, 5*5*20]) conn = tf.matmul(fc, dense) # out,输出层 W = np.random.randn(120, 9) b = np.random.randn(9) out = tf.matmul(conn, W) + b