Chessboard
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 16924 | Accepted: 5284 |
Description
Alice and Bob often play games on chessboard. One day, Alice draws a board with size M * N. She wants Bob to use a lot of cards with size 1 * 2 to cover the board. However, she thinks it too easy to bob, so she makes some holes on the board (as shown in the figure below).
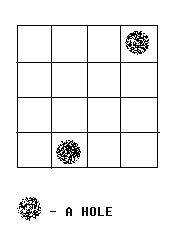
We call a grid, which doesn’t contain a hole, a normal grid. Bob has to follow the rules below:
1. Any normal grid should be covered with exactly one card.
2. One card should cover exactly 2 normal adjacent grids.
Some examples are given in the figures below:
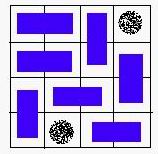
A VALID solution.
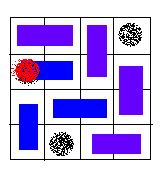
An invalid solution, because the hole of red color is covered with a card.
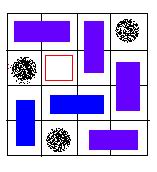
An invalid solution, because there exists a grid, which is not covered.
Your task is to help Bob to decide whether or not the chessboard can be covered according to the rules above.

We call a grid, which doesn’t contain a hole, a normal grid. Bob has to follow the rules below:
1. Any normal grid should be covered with exactly one card.
2. One card should cover exactly 2 normal adjacent grids.
Some examples are given in the figures below:

A VALID solution.

An invalid solution, because the hole of red color is covered with a card.

An invalid solution, because there exists a grid, which is not covered.
Your task is to help Bob to decide whether or not the chessboard can be covered according to the rules above.
Input
There are 3 integers in the first line: m, n, k (0 < m, n <= 32, 0 <= K < m * n), the number of rows, column and holes. In the next k lines, there is a pair of integers (x, y) in each line, which represents a hole in the y-th row, the x-th column.
Output
If the board can be covered, output "YES". Otherwise, output "NO".
Sample Input
4 3 2 2 1 3 3
Sample Output
YES
思路:将两个相邻的grid建边,判断二分图最大匹配*2+k是否等于n*m
#include <cstdio> #include <cstring> #include <vector> using namespace std; const int MAXN=40; const int MAXV=1100; int n,m,k; int mz[MAXN][MAXN]; int dy[4]={0,1,0,-1}; int dx[4]={1,0,-1,0}; vector<int> arc[MAXV]; int vis[MAXN][MAXN]; int match[MAXV],used[MAXV]; bool dfs(int u) { for(int i=0;i<arc[u].size();i++) { int to=arc[u][i]; if(!used[to]) { used[to]=1; int w=match[to]; if(w==-1||dfs(w)) { match[to]=u; match[u]=to; return true; } } } return false; } int max_flow() { int ans=0; memset(match,-1,sizeof(match)); int limit=n*m; for(int i=1;i<=limit;i++) { if(match[i]==-1) { memset(used,0,sizeof(used)); if(dfs(i)) { ans++; } } } return ans; } int main() { while(scanf("%d%d%d",&n,&m,&k)!=EOF) { if((n*m-k)%2!=0) { printf("NO "); continue; } for(int i=0;i<MAXV;i++) arc[i].clear(); memset(vis,0,sizeof(vis)); memset(mz,0,sizeof(mz)); for(int i=0;i<k;i++) { int x,y; scanf("%d%d",&x,&y); mz[y][x]=-1; } //int edge=0; for(int y=1;y<=n;y++) { for(int x=1;x<=m;x++) { vis[y][x]=1; if(mz[y][x]==-1) continue; for(int i=0;i<4;i++) { int ny=y+dy[i]; int nx=x+dx[i]; if(1<=ny&&ny<=n&&1<=nx&&nx<=m&&mz[ny][nx]!=-1&&!vis[ny][nx]) { // edge++; int u=(y-1)*m+x; int v=(ny-1)*m+nx; arc[u].push_back(v); arc[v].push_back(u); } } } } //printf("%d ",edge); int res=max_flow(); if(res*2+k==n*m) { printf("YES "); } else { printf("NO "); } } return 0; }