
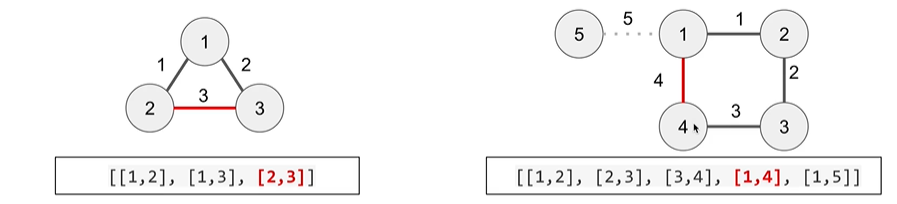
思路:
记录1到N的每个数的根,因为如果有环,导致环相连的[u, v]一定有相同的root,
我们可以理解为是一个节点的两个分支,通过[u,v]被连起来了,既然他们是一个节点的两个分支,那么他们一定有相同的root,所以直接移除[u,v]就好啦。
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
# 并查集
root = [i for i in range(len(edges)+1)]
# 找根节点
def find(i):
# 根节点就是自身
if i != root[i]:
root[i] = find(root[i])
return root[i]
for u, v in edges:
u_parent = find(u)
v_parent = find(v)
if u_parent != v_parent:
root[v_parent] = u_parent
else:
return [u, v]



case2.1虽然没有构成环,但是node 3有两个parent,分别是1, 2,因此也要删除一条边
构成环的,就要将构成环的边删除
case2.2 为什么不是删除1,4这条边,因为1节点有两个父节点,因此要删除两个父节点的那条边,所以删除1,2这条边
上一道题解说过,无向图能构成一棵树的条件是没有环,那么有向图的条件是什么呢?
首先还是得没有环,其次因为是边是有向的,所以一个结点只能有一个父结点(也就是入度为 )。那么这题解法就有了。
- 首先判断有没有入度为
的结点,如果有的话,那两条边一定有一条得删掉。
- 按照出现时间从后到前看那两条边,删掉其中一条之后是否能构成一棵树(也就是无环)。如果删掉了无环,那就直接返回这条边作为答案。
- 如果入度全是
,那就直接按照出现时间从前到后看添加了哪一条边之后开始出现了环,那么那条边就是答案。
判断能否构成一棵树的话还是用并查集,唯一区别就是不需要用按秩合并的优化了,而且给定有向边 ,只能把
接在
下面。
class Solution:
def __init__(self):
self.n = 0
self.f = []
def findRedundantDirectedConnection(self, edges):
self.n = len(edges)
degree = [0] * (self.n + 1)
for u, v in edges:
degree[v] += 1
for u, v in edges[::-1]:
if degree[v] == 2 and len(self.wrongEdge(edges, [u, v])) == 0:
return [u, v]
return self.wrongEdge(edges, [])
def wrongEdge(self, edges, ex):
self.f = [i for i in range(self.n + 1)]
for u, v in edges:
if [u, v] == ex:
continue
if self.same(u, v):
return [u, v]
self.join(u, v)
return []
def find(self, u):
if u == self.f[u]:
return u
self.f[u] = self.find(self.f[u])
return self.f[u]
def join(self, u, v):
u, v = self.find(u), self.find(v)
if u == v:
return
self.f[v] = u
def same(self, u, v):
u, v = self.find(u), self.find(v)
return u == v