C语言进制之间转换

课程导言

【最早的编程语言是二进制语言，也是计算机能够直接识别的唯一语言。不管用什么高级语言编写的程序最后都要转换为二进制语言，才能在计算机上执行，因此掌握二进制知识对学习编程语言是非常有帮助的。本篇和同学们探讨二进制计数原理以及与十进制、十六进制的转换。通过本篇的学习，你将了解到为什么计算机能够直接识别二进制语言，二进制的计数原理以及与十进制、十六进制之间的数值转换。】

在讲述二进制之前，先做一个小游戏。伸出我们的右手，从小指开始，依次到大拇指分别代表数字1、2、4、8、16。并且每个手指分为两种状态，手指伸直为1状态，手指弯曲为0状态。然后分别做每个手指自由伸直或弯曲动作，记录其状态和每个手指的数字之和，状态顺序从大拇指开始：

（1）动作：伸直小指、中指和大拇指，弯曲无名指和食指。

状态：10101        

数字之和：21

（2）动作：伸直小指、无名指和中指，弯曲大拇指和食指。

状态：00111        

数字之和：7

（3）动作：伸直全部手指。

状态：11111        

数字之和：31

有同学可能会问，做这个游戏的意义在什么地方呢？这个游戏用直观化的方式演示了二进制数到十进制数的转换，五个手指的伸直和弯曲的状态组合用0和1表述出来，就是我们本课程要探讨的二进制数，游戏中记录的数字之和就是二进制数的十进制表示。

前面的游戏可以把5个二进制数转换为十进制数，同样的道理，也可以把30以内的十进制数转换为二进制数。只需要把十进制数分解成16、8、4、2、1任意数字之和就可以，然后将对应数字的右手手指伸直，没有对应数字的右手手指弯曲，从大拇指开始记录其组合状态，该组合状态就是要转换的二进制数。

例如：

十进制数字：5=4+1   对应的二进制数为：00101

十进制数字：28=16+8+4   对应的二进制数为：11100

前面的游戏能不能实现更多二进制数的转换呢？当然可以，右手五个手指表示5个二进制数，如果再加上左手就可以表示10个二进制数了，所能表示的十进制数也更大。依次类推，多人合作可以表示更多位的二进制数和更大的十进制数。

从前面的游戏中可以看出，二进制数只有两个状态0和1，二进制数的这个特质非常适合描述电路的通与短、开关的打开与关闭，计算机的电路都是由电子器件组成的，电子器件的状态也分为0（低电位）和1（高电位），二进制的特征正好满足了计算机中电子器件的运算要求，因此计算机内部运算都采用二进制运算，能够识别的数也是二进制数。

计算机能够识别的数制是二进制数，二进制数是用0和1两个数字来表示的数，计算机的指令集也是采用二进制表示，机器语言就是用二进制数来编写程序。

可以借助十进制数来理解二进制数。在十进制中，最开始学习的是十以内的加法，之后是两位数的加法，在两位数加法的学习中，就需要逢十进一了，按进位的原则进行记数的方法叫做进位记数制，也称为“数制”或“进制”。

我们平时用的最多的就是十进制，时间是六十进制，也就是说逢六十进一，例如60秒进1分，60分进1小时。因此每一种数制的进位都遵循一个规则，那就是——逢n进1。这里的n叫做基数。

在十进制中，每一位有0、1、2、3、4、5、6、7、8、9十个数码，因此基数为10，超过9就必须用多位数来表示，并遵循逢十进一的原则。一个任意的十进制数可以表示为：

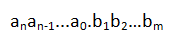
其含义是：

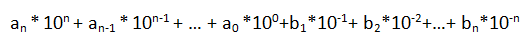
其中ai（i=0,1…,n）,bj（j=1,2,…,m）是0、1、2、3、4、5、6、7、8、9十个数码中的一个。

上式中相应于每位数字的10n称为该数字的权，其大小是以基数为底，数码所在位置的序号为指数的整数次幂。

例如：十进制数1111.111

这个十进制数的7个位数虽然都是1，但是每个位数1表示的数值意义不同，从左往右数第一个1表示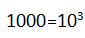，第二个1表示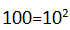

，……，第7个1表示0.001=10-3，每个位数表示的数值叫做位权，也就是基数的n幂。十进制数1111.111以小数点为界，整数部分自右向左，依次是基数的0次、1次、2次、3次幂。小数部分，自左向右，分别是基数的-1次、-2次、-3次幂。每位数字乘以其权所得的乘积之和即为所表示数的值。

例如：

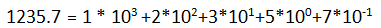
十进制是人们最熟悉、最常用的一种数制，但它不是唯一的数制。例如计时用的时、分、秒就是按60进制计数的。基数为r的r进制数可以表示为：

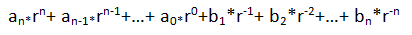
二进制和十六进制数

计算机就其本身来说是一个电器设备，为了能够快速存储、处理、传递信息，其内部采用了大量的电子元件，在这些电子元件中，电路的通和断、电压高低，这两种状态最容易实现，也最稳定、也最容易实现对电路本身的控制。计算机工程师将计算机所能表示这样的状态，用0，1来表示、即用二进制数表示计算机内部的所有运算和操作。二进制数运算非常简单，计算机很容易实现，所以计算机内部都用二进制编码进行数据的传送和计算。

二进制的基数为2，只有0、1两个数码，并遵循逢二进一的原则，它的各位权是以2k表示的，因此二进制数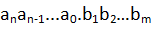的值为：

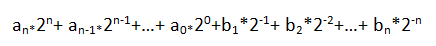
其中ai，bj为0、1两个数码中的一个。例如：

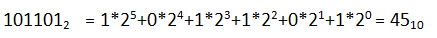
其中数的下标表示该数的基数r，即二进制的101101与十进制的45等值。

n位的二进制数可以表示2n个数。例如：3位二进制数可以表示8个数，分别是：

1.  
   二进制数 相对应的十进制数
2.  
   000 0
3.  
   001 1
4.  
   010 2
5.  
   011 3
6.  
   100 4
7.  
   101 5
8.  
   110 6
9.  
   111 7

而4位二进制数则能表示十进制的0 ~ 15共16个数如下：

二进制数    相对应的十进制数
0000          0
0001          1
0010          2
0011          3
0100          4
0101          5
0110          6
0111          7
1000          8
1001          9
1010          10
1011          11
1100          12
1101          13
1110          14
1111          15

为了方便阅读及书写，经常使用十六进制来表示二进制数，十六进制的基数是16，数码为0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F，其中用A，B，C，D，E，F（字母不区分大小写）这六个字母来分别表示10，11，12，13，14，15。

按同样的方法，可以很容易地掌握十六进制数的表示方法。例如：

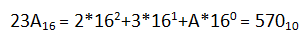
在计算机编程语言中，通常用数字后面跟一个英文字母来表示该数的数制。十进制一般用D（Decimal）、二进制数用B（Binary）、十六进制用H（Hexadecimal）来表示。例如：23AH、570D、110101B、0075H，…。当然也可以用这些字母的小写形式。

不同进制数的相互转换

计算机中采用的是二进制，但用计算机解决实际问题时对数值的输入输出通常使用十进制，这就有一个十进制向二进制转换或由二进制向十进制转换的过程。也就是说，在使用计算机进行数据处理时首先必须把输入的十进制数转换成计算机所能接受的二进制数；计算机在运行结束后，再把二进制数转换为人们所习惯的十进制数输出。

1、二进制数转换成十进制数  

 把二进制数转换成十进制数就是用“按权相加法”，把二进制数首先写成加权系数展开式，然后按十进制加法规则求和。

 例：把二进制数110.11转换成十进制数。 

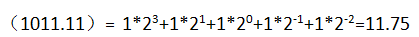
2、十进制数转换为二进制数 

  前面“按权相加法”中，权的值在小数点左边和小数点右边是不一样的。所以，十进制数转换为二进制数时，整数和小数的转换方法也不同，一般先把十进制数的整数部分和小数部分分别转换后，再加以合并。

十进制整数转换为二进制整数采用"除2取余，逆排序"法。具体做法是：用2去除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行，直到商为零时为止，然后把所有余数按逆序排列，也就是把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。这就是所谓“除2取余，逆序排列”。

例：将一个十进制数25转换为二进制数。

              

                               

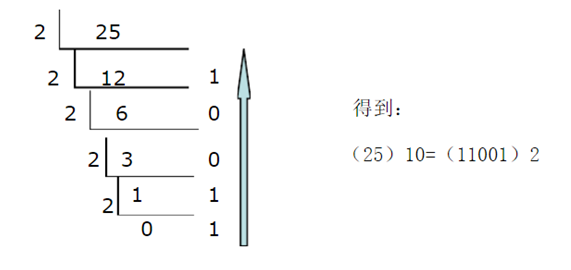
3、十六进制和二进制之间的转换

由于十六进制的基数是2的幂，所以这两种数制之间的转换是十分容易的。一个二进制数，只要把它从低位到高位每4位组成一组，直接用十六进制数来表示就可了。

例：0011  0101  1011  1111 = 35BF

      3     5     B     F

反之，把十六进制数中的每一位用4位二进制数表示，就形成相应的二进制数了。

              A     1     9     C

例：A19C = 1010  0001  1001  1100

4、十六进制数转换为十进制数

同二进制数转换十进制数相同，各位十六进制数与其对应权值的乘积之和即为与此十六进制相对应的十进制数。

十进制数转换为十六进制数也可使用除法进行。

二进制数是逢二进位的进位制，0、1是基本算符，计算机运算基础采用二进制。编程过程中经常会用到十六进制，而十进制的使用非常少，这是因为十六进制和二进制有天然的联系：四个二进制位可以表示从0到15的数字，这刚好是1个16进制位可以表示的数据，也就是说，将二进制转换成十六进制只要每4位进行转换就可以了。

■ 课程小结

1、二进制只有两个数字，就是0和1，类似开关的接通和断开。计算机里面的芯片都是电子电路，也只有两种状态，高电位（通电）和低电位（断电），因此用二进制表示电子电路的状态是最合适不过了，不用任何翻译过程，电子电路会自动识别用二进制语言写的代码。

2、二进制和其它进制是可以互相转换的，如十进制和十六进制，具体转换方法课程已经介绍的比较详细了。这里主要说一说为什么进制间要相互转换？我们知道计算机内部是用二进制表示的，但人们用计算机工作时，输入的都是十进制数和字符，这就需要把人们输入的数据通过处理程序转换为计算机能够识别的二进制数。同样的道理，当人们需要从计算机查询信息时，处理程序就需要把二进制数转换成人们能够容易识别的十进制数或者字符。

从转换过程看，好像没有十六进制的事，其实十六进制是为了方便编程人员编写代码而提供的，主要是在编程语言中，用十六进制表示数值特别方便，可以以较少的数位表示较大的数，而且十六进制和二进制的转换也非常方便，因此程序员更喜欢在代码中用十六进制表示数值。

■ 思考与练习

1、将下列二进制数转换为十六进制数和十进制数：

（1）10101   （2）10000000  （3）11111111

2、用除法将下列十进制数转换为二进制数和十六进制数：

（1）369    （2）10000   （3）4095

3、将下列十六进制数转换为二进制数和十进制数：

（1）FA     （2）5B     （3）F234