51nod 2583

题意

51nod

做法

在(gcd(x,y))的过程中，仅有第一次可能出现(xle y)的情况
下面假定(x>y)

考虑一棵递归的树，节点是二元组((a,b)(a>b,ale m))。((a,b)longrightarrow (a',b'))则令((a',b'))为((a,b))的父亲
点((a,b))的子树：

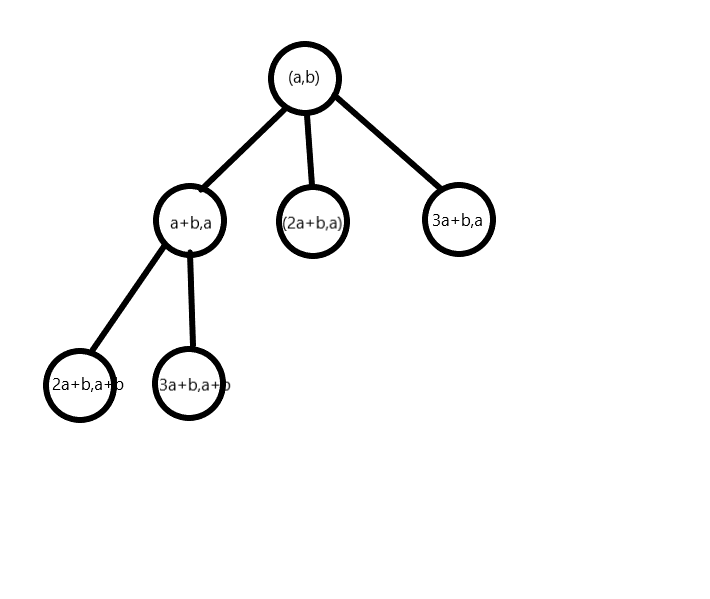
然后就可以把((a,b))的子树可以通过，以下两种操作得出：

((a,b)longrightarrow (a+b,b))，((a,b)longrightarrow (a,a+b))

用二元组((p,q))描述一个数(px+q(x+y))，因为((x,y))是不能向右走，为方便计算，先往下走一步((x,x+y))，则可以用(((1,0),(0,1)))描述出来
以下两种操作得出：

(((a,b),(c,d))longrightarrow ((a+c,b+d),(b,d)))
(((a,b),(c,d))longrightarrow ((a,b),(a+c,b+d)))

Sbtree每行相邻两点对应了一个(((a,b),(c,d)))

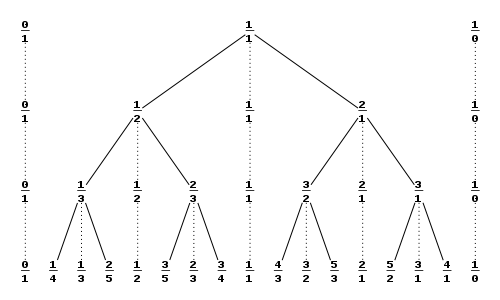
那么树上一个点对应了两个贡献
所以算，(2 imes sumlimits_{i,j}[gcd(i,j)=1][xi+(x+y)j le m])