[集训]Trominoes，钩子公式运用

题意

用这四种骨牌密铺n*m的正方形矩阵，可以不选，求方案数。n*m<=1E8。多组询问。

---

思考

用如上的表达难以进行计算，尝试转化为一种新的组合解释。

若从右上角开始填起，我们强制要求里面的轮廓线是单调增的。例如：

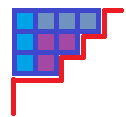这种方法既不影响合法性，又不会重复计数。

可以看见，我们只关心轮廓线的形状，不关心其他部分的细节，因此我们可以用长度为n+m的01串来表示其反向。在此处，默认01串从左下角向右上角写起，0代表上，1代表右。

每填充一个骨牌，可以发现这样的转移：

0001->1000

0011->1010

0101->1100

0111->1110

除了第四位上的数字，其余的三位在二进制表示下是完备的，也就是说，可以看做是单一的1先前移动了3位。

至此，原问题表述为：给定一个开头有n个1，末尾有m个0的字符串，每次可将1向前移动三位到一个字符为0的位置上，问构成开头有m个0，末尾有n个1的字符串的方案数有多少个。

该问题又可以划分为三个子问题，因为位置模3的余数不同的互不影响。也就是考虑若每次向右移动一个，有多少方案。

这个问题可以看做是经典的买票问题，使用钩子公式解决。复杂度O(n*m/3+T*n)

---

代码

#include<bits/stdc++.h>
#define mod 1000000007
using namespace std;
typedef long long int ll;
ll fac[33333335],n,m,T;
void init()
{
    fac[0]=1;
    for(int i=1;i<=33333333;++i)
        fac[i]=fac[i-1]*i%mod;
}
ll qpow(ll x,ll y)
{
    ll ans=1,base=x;
    while(y)
    {
        if(y&1)
            ans=ans*base%mod;
        base=base*base%mod;
        y>>=1;
    }
    return ans;
}
inline ll C(int x,int y)
{
    return fac[x]*qpow(fac[y],mod-2)%mod*qpow(fac[x-y],mod-2)%mod;
}
inline ll get(ll n,ll m)
{
    ll ans=1,sum=1;
    for(int i=1;i<=n;++i)
    {
        ans=ans*fac[i+m-1]%mod;
        sum=sum*fac[i-1]%mod;
//        for(int j=1;j<=m;++j)
//            ans=ans*(i+j-1)%mod;
    }
    return fac[n*m]*qpow(ans,mod-2)%mod*sum%mod;
}
int main()
{
    ios::sync_with_stdio(false);
    init();
    cin>>T;
    while(T--)
    {
        cin>>n>>m;
        if(n*m%3!=0)
        {
            cout<<0<<endl;
            continue;
        }
        if(n%3!=0)
            swap(n,m);
        int base0=m/3;
        int left0=base0,left1=base0+(m%3>0),left2=base0+(m%3>1);
        ll ans=get(n/3,left0)*get(n/3,left1)%mod*get(n/3,left2)%mod;
        ans=ans*C((left0+left1+left2)*n/3,left0*n/3)%mod;
        ans=ans*C((left1+left2)*n/3,left1*n/3)%mod;
        cout<<ans<<endl;
    }
    return 0;
}