[Luogu P3959] 宝藏 (状压DP+枚举子集)

题面

传送门：https://www.luogu.org/problemnew/show/P3959

---

Solution

这道题的是一道很巧妙的状压DP题。

首先，看到数据范围，应该状压DP没错了。

根据我们之前状压方程的设计经验，我们很快就能设计出这样的方程：

设f[i][j]表示用到第i个元素，当前连接状态为j的开销的min

但是我们很快就会发现，这个方程没法转移，因为随着连接方案的不同，新插入的点的K值会不同。

怎么办呢？

这时候我们可以重新设计一个巧妙的的状态。

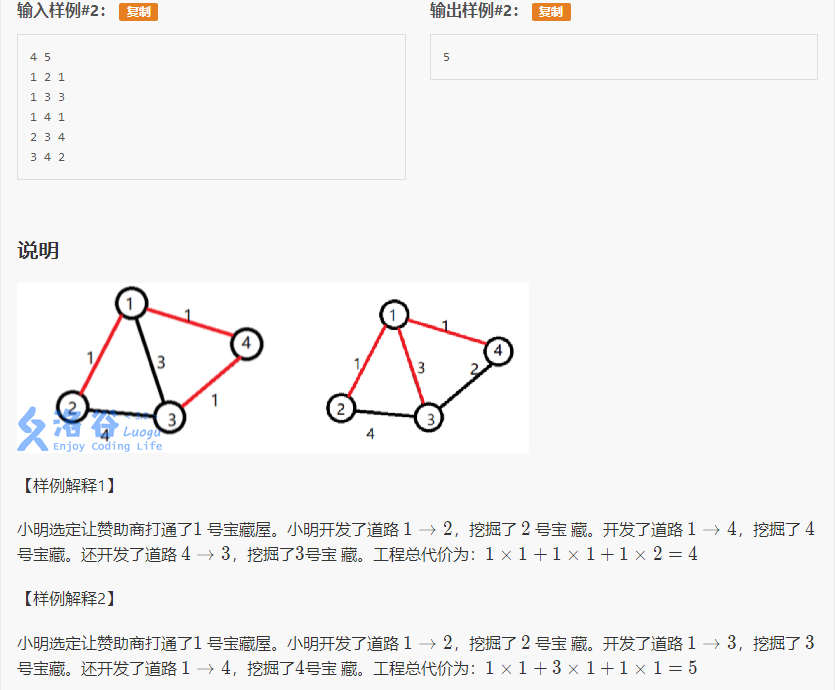
重新阅读题目，我们可以发现题目中的K值可以理解为距离初始点的“层数”，下面这幅图可以简单的表示出来：

那么，我们可以考虑这样子设状态：

设f[i][j]表示到第i层，总共取了的点的状态为j。

这样的话，转移就可以取出来了：

f[i][j]=MIN(f[i-1][k]+trans[k][j]*(i-1)) (k为j的子集，即有可能转移到j的状态) (trans[k][j]表示从状态k转移到状态j的最小花费的路程)

trans需要暴力预处理出来。

怎么枚举子集呢？

如果2^n枚举就会T掉，因为我们枚举到了非子集的情况。

这里就引出了枚举子集的小技巧

对于状态x，它的子集为：p=x,p!=0,p=(p-1)&x (至于怎么证明，这里就不给出了，在草稿上推一推就会发现里面的精妙了)

答案就是min(f[i][2^n-1])，初始化f[1][2^(i-1)]=0 (i∈[1,n])

就酱，这道题就被我们切掉啦φ(>ω<*) 

---

Code

//Luogu P3959 宝藏 
//Sep,5th,2018
//状压DP+枚举子集小技巧
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long read()
{
    long long x=0,f=1; char c=getchar();
    while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}
    return x*f;
}
const int N=12+2;
const int M=1<<N;
int n,m,dis[N][N],trans[M][M],POW[N];
long long f[N][M];
int main()
{
    n=read(),m=read();
    memset(dis,0x3f,sizeof dis);
    for(int i=1;i<=m;i++)
    {
        int s=read(),t=read(),v=read();
        if(dis[s][t]>v)
            dis[s][t]=dis[t][s]=v;
    }
    
    m=(1<<n);
    POW[0]=1;
    for(int i=1;i<=n;i++)
        POW[i]=POW[i-1]*2;
    for(int i=0;i<m;i++)
        for(int j=i;j!=0;j=(j-1)&i)
        {
            bool OK=true;
            int temp=i^j;
            for(int k=n-1;k>=0;k--)
                if(temp>=POW[k])
                {
                    int tmin=0x3f3f3f3f;
                    for(int o=1;o<=n;o++)
                        if((POW[o-1]&j)==POW[o-1])
                            tmin=min(tmin,dis[o][k+1]);
                    if(tmin==0x3f3f3f3f)
                    {
                        OK=false;
                        break;
                    }
                    trans[j][i]+=tmin;
                    temp-=POW[k];
                }
            if(OK==false)
                trans[j][i]=0x3f3f3f3f;
        }
        
    /*cerr<<endl<<endl;
    for(int i=0;i<m;i++)
        for(int j=0;j<m;j++)
            if(trans[i][j]!=0x3f3f3f3f and trans[i][j]!=0)
                cerr<<i<<" "<<j<<" "<<trans[i][j]<<endl;*/
    
    memset(f,0x3f,sizeof f);
    for(int i=1;i<=n;i++)
        f[1][POW[i-1]]=0;
    for(int i=2;i<=n;i++)
        for(int j=0;j<m;j++)
            for(int k=j;k!=0;k=(k-1)&j)
                if(trans[k][j]!=0x3f3f3f3f)
                    f[i][j]=min(f[i][j],f[i-1][k]+(i-1)*trans[k][j]);
    
    long long ans=0x3f3f3f3f3f3f3f3fll;
    for(int i=1;i<=n;i++)
        ans=min(ans,f[i][m-1]);
    printf("%lld",ans);
    return 0;
}