定义
竞赛图:\(n\) 个点的竞赛图定义为将 \(n\) 个点的无向完全图每条边任意定向所构成的有向图。
为什么称之为竞赛图呢?因为其存在一个组合意义:\(n\) 只队伍两两之间比赛,每场比赛从赢的向输的连边就构成了一张竞赛图。
性质
性质一:竞赛图缩点后呈链状
注意,这里的链状并不是直接呈一条链,而是类似于 \(n\) 个点链状偏序集,任意两个强连通分量之间从拓扑序小的连向拓扑序大的,如下图所示。
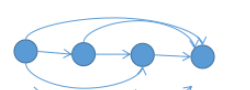
证明考虑缩点之后的图等价于一个新的 \(n\) 个点没有环的竞赛图,那么一定存在一个拓扑序,拓扑序上连边必定为链状(这里归纳)。
性质二:竞赛图每个强连通分量存在哈密顿回路
考虑对点数归纳(注意不存在 \(n = 2\) 的强连通竞赛图),等价于:向一个强连通竞赛图加入一个点,证明存在一条包含所有点的哈密顿回路。
找到 \(n - 1\) 个点时的哈密顿回路,那么定能在上面找到相邻两个点 \(u \to v\) 使得存在边 \(u \to n, n \to v\),这样就能接上去了。
若不存在这样的一对相邻点,那么环上每个点要么都连向 \(n\),要么都从 \(n\) 连向这些点,显然 \(n\) 与这些点不强连通。
性质三:竞赛图存在一条哈密顿路径
根据性质一,考虑缩点后按照拓扑序构造哈密顿路径。
根据性质二,任选一个强连通分量内的哈密顿回路然后走到拓扑序上下一个强连通分量即可。
性质四(性质二拓展):对于竞赛图的一个大小为 \(n(n \ge 3)\) 的强连通分量,其一定存在大小 \(\forall l \in [3, n]\) 的简单环
首先这个命题等价于弱化结论:对任意一个强连通竞赛图成立即可。
任然考虑对强连通竞赛图点数归纳,根据性质二,每次能找到一个长为 \(n\) 的哈密顿回路,因此此时覆盖完了 \([3, n]\)。
性质五(兰道定理):存在竞赛图满足每个点出度序列为 \(s\) 当且仅当:
- 将 \(s\) 从小至大排序,\(\forall k \in [1, n], \sum\limits_{i = 1} ^ k s_i \ge \binom{k}{2}\) 且 \(k = n\) 时等号成立。
必要性显然,考虑证明充分性。
考虑从一个特殊的出度序列 \(a\) 开始不断调整直到 \(a\) 与 \(s\) 相同。
这个特殊的出度序列为 \(a = (0, 1, \cdots n - 1)\),显然 \(a\) 是可以被构造得出的。
首先若 \(a\) 还没有与 \(s\) 完全相等,那么我们定可以找到一个最小的位置 \(x\) 使得 \(a_x < s_x\),我们考虑将 \(a_x\) 扩大直到与 \(s_x\) 相等。
此时,我们找到从 \(x\) 开始在 \(a\) 中极长的相等的段 \(a_x \cdots a_y\) 使得 \(a_x = a_{x + 1} = \cdots = a_y\)。
然后再找到最小 \(z\) 使得 \(a_z > s_z\),由于 \(s\) 不降,那么定有 \(z > y\)。
于是我们发现:\(a_z > s_z \ge s_y > a_x\),因此有 \(a_z - a_x \ge 2\)。
这意味着至少存在一个点 \(p(p \ne z, p \ne x)\) 使得 \(z \to p, p \to x\)(注意需要考虑 \(z \to x\),因此差值至少要 \(\ge 2\))
我们将 \(z \to p, p \to x\) 的边反转,此时 \(a_x \leftarrow a_x + 1, a_z \leftarrow a_z - 1\)。
因此我们实现了将 \(a_x + 1\),容易发现这样一定可以保证相等的前缀不动且逐渐扩展这个前缀,因此一定可以构造完成。