银河英雄传说
这是一道带权并查集的题目。
首先,按照题目要求,我们可以很容易的想到用并查集来实现。但是我们会发现,如果只用并查集记录队列的合并情况,那么就无法满足C操作,所以我们需要在维护并查集的同时,维护每个结点的信息。
这道题目需要查询是否在一个队列中,也就是是否在一个集合中,是并查集的基本操作,写一个find函数就可以了。但是第二个要求是一个并查集中两个结点的距离,那么我们就需要一个d数组,记录结点i到fa[i]的距离,那么询问的时候就可以输出abs(d[x]-d[y])-1。
那接下来的问题就是怎么维护这个d数组呢?首先我们可以明确的一点是需要在查询、合并并查集的时候维护,那我们想一想,并查集在合并的时候,会把一个并查集的头结点和另一个并查集的头结点合并,但是题目的要求是,把一个并查集的头部接到另一个并查集的尾部,所以我们就需要知道并查集的大小,我们用siz表示,这样的话每次合并我们就只需要做和就可以了,因为结点到新队列头结点的距离=当前节点原来到队头的距离+新并查集的大小。如果不理解的话,我们可以看一下下面的图:
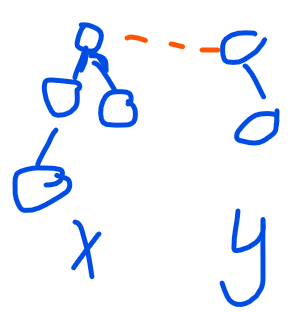
当我们要合并x和y的时候,我们会把两个并查集的头结点连接起来,所以x中子节点的d就可以表示为y的大小+它到x头结点的距离。
下面是AC代码:
#include<bits/stdc++.h> #define R register int #define M 500500 using namespace std; int t,fa[M],d[M],siz[M]; //d 表示飞船i到队头的距离 siz 表示飞船所在并查集的大小 char ch; inline int find(int x){ if(fa[x]!=x){ int k=fa[x]; fa[x]=find(fa[x]); d[x]+=d[k]; //当前结点到新队列头结点的距离=当前节点原来到队头的距离+队头到新队列头的距离 siz[x]=siz[fa[x]]; //更新当前集合的大小 } return fa[x]; } inline void add(int x,int y){ int fx=find(x),fy=find(y); fa[fx]=fy; d[fx]=d[fy]+siz[fy]; //前结点到新队列头结点的距离=当前节点原来到队头的距离+新并查集的大小 siz[fy]+=siz[fx]; siz[fx]=siz[fy]; } inline int query(int x,int y){return find(x)!=find(y) ? -1 : abs(d[x]-d[y])-1;} int main(){ ios::sync_with_stdio(0); int x,y; cin>>t; for(R i=1;i<=30000;++i) fa[i]=i,siz[i]=1; while(t--){ cin>>ch>>x>>y; if(ch=='M') add(x,y); else cout<<query(x,y)<<endl; } return 0; }